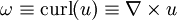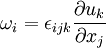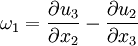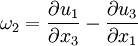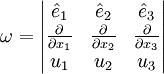Vorticity
From CFD-Wiki
Vorticity is a vector field variable which is derived from the velocity vector. Mathematically, it is defined as the curl of the velocity vector
In tensor notation, vorticity is given by:
where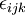 
is the alternating tensor. The components of vorticity in Cartesian coordinates are;:
This can be obtained by using determinants
where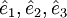 
are the unit vectors for the Cartesian coordinate system.
Physical Significance
The vorticity can be seen as a vector having magnitude equal to the maximum "circulation" at each point and to be oriented perpendicularly to this plane of circulation for each point.
