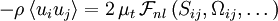Nonlinear eddy viscosity models
From CFD-Wiki
This is class of turbulence models for the RANS equations in which an eddy viscosity coefficient is used to relate the mean turbulence field to the mean velocity field, however in a nonlinear relationship
where
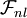 is a nonlinear function possibly dependent on the mean strain and vorticity fields or even other turbulence variable
is a nonlinear function possibly dependent on the mean strain and vorticity fields or even other turbulence variable
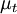 is the coefficient termed turbulence "viscosity" (also called the eddy viscosity)
is the coefficient termed turbulence "viscosity" (also called the eddy viscosity)
![S_{ij}= \frac{1}{2} \left[ \frac{\partial U_{i}}{\partial x_{j}} + \frac{\partial U_{j}}{\partial x_{i}} \right] - \frac{1}{3} \frac{\partial U_{k}}{\partial x_{k}} \delta_{ij}](/W/images/math/b/c/3/bc3208f532c9a8eeac8e38becd118e0a.png) is the mean strain rate
is the mean strain rate
![\Omega_{ij}= \frac{1}{2} \left[ \frac{\partial U_{i}}{\partial x_{j}} - \frac{\partial U_{j}}{\partial x_{i}} \right]](/W/images/math/9/e/1/9e1326960c808cde3078bf2d87d93a13.png) is the mean vorticity
is the mean vorticity

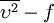 model
model
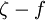 model
model