Lift and drag
From CFD-Wiki
The force on a body immersed in a fluid is decomposed into lift and drag. Lift is the component of the force normal to the freestream velocity while drag is the force in the direction of the freestream velocity.
The force on a body 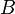 can be obtained by integrating the stress on the surface
can be obtained by integrating the stress on the surface 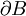 of the body and is given by
of the body and is given by
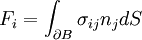
where
-
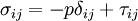 is the total stress
is the total stress
-
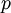 is the static pressure
is the static pressure
-
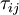 is the shear stress
is the shear stress
-
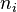 is the unit normal vector to
is the unit normal vector to 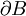
If 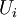 is the freestream velocity with
is the freestream velocity with 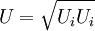 then the drag force (
then the drag force (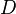 ) is given by
) is given by
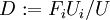
The remaining force can be considered as lift force. For a 3-D slender body the lift force may be broken into a normal force and a side force.
In 2-D, the lift (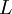 ) and drag are given by
) and drag are given by
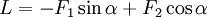
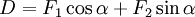
where 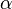 is the angle of attack, that is the angle between the freestream velocity and the
is the angle of attack, that is the angle between the freestream velocity and the 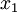 axis.
axis.
