Johnson-King model
From CFD-Wiki
It is also categorized as half-equation model, because it essentially solves for an Ordinary Differential Equation (ODE) rather than a Partial Differential Equation (PDE) (Normally for popular turbulence models transport equations are solved which are PDE's). This model solves for a transport equation for the maximum shear stress. It was not developed to be a universal model, rather to solve only for turbulent boundary layer flows with strong adverse pressure gradient.
References
- Johnson, D.A. and King, L.S. A mathematically simple turbulence closure model for attached and separated turbulent boundary layers, AIAA Journal, 23, 1684-1692, 1985.

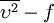 model
model
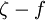 model
model