Combustion
From CFD-Wiki
What is combustion -- physics versus modelling
Combustion phenomena consist of many physical and chemical processes which exhibit a broad range of time and length scales. A mathematical description of combustion is not always trivial, although some analytical solutions exist for simple situations of laminar flame. Such analytical models are usually restricted to problems in zero or one-dimensional space.
Most problems in combustion involve turbulent flows, gas and liquid fuels, and pollution transport issues (products of combustion as well as for example noise pollution). These problems require not only extensive experimental work, but also numerical modelling. All combustion models must be validated against the experiments as each one has its own drawbacks and limits. In this article, we will address the modeling fundamentals only.
In addition to the flow parameters used in fluid mechanics,
new dimensionless parameters are introduced, the most important of which are the Karlovitz number and the Damkholer number which represent ratios of chemical and flow time scales, and
the Lewis number which compares the diffusion speeds of species.
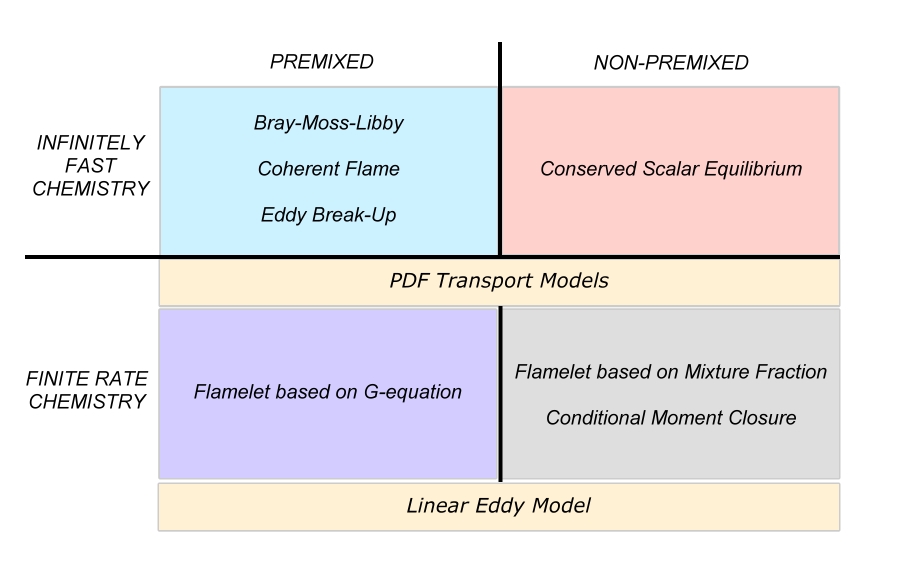
The combustion models are often classified on their capability to deal with the different combustion regimes.
Three Combustion Regimes
Depending on how fuel and oxidizer are brought into contact in the combustion system, different combustion modes or regimes are identified. Traditionally, two regimes have been recognized: the premixed regime and the non-premixed regime. Over the last two decades, a third regime, sometime considered as a hybrid of the two former ones to a certain extend, has risen. It has been named partially-premixed regime.
The Non-Premixed Regime
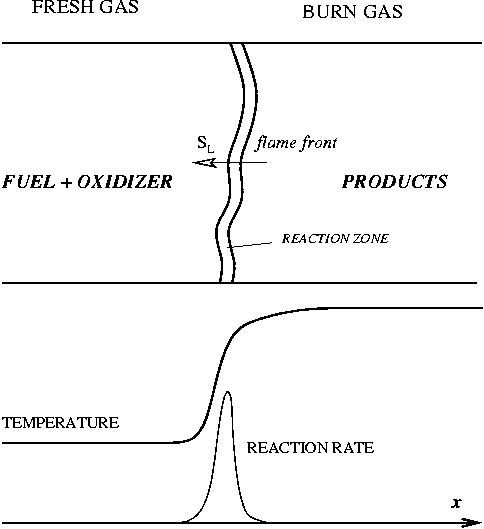
This regime is certainly the easiest to understand. Everybody has already seen a lighter, candle or gas-powered stove. Basically, the fuel issues from a nozzle or a simple duct into the atmosphere. The combustion reaction is the oxidization of the fuel. Because fuel and oxidizer are in contact only in a limited region but are separated elsewhere (especially in the feeding system) this configuration is the safest. The non-premixed flame has some other advantages. By controlling the flows of both reactants, it is (theoretically) possible to locate the stoichiometric interface, and thus, the location of the flame sheet. Moreover, the strength of the flame can also be controlled through the same process. Depending on the width of the transition region from the oxidizer to the fuel side, the species (fuel and oxidizer) feed the flame at different rates. This is because the diffusion of the species is directly dependent on the unbalance (gradient) of their distribution. A sharp transition from fuel to oxidizer creates intense diffusion of those species towards the flame, increasing its burning rate. This burning rate control through the diffusion process is certainly one of the reasons of the alternate name of such a flame and combustion mode: diffusion flame and diffusion regime.
The Premixed Regime
In contrast to the non-premixed regime above, the reactants are here well mixed before entering the combustion chamber. Chemical reaction can occur everywhere and this flame can propagate upstream into the feeding system. This presents lots of safety issues. Some situations prevent them: (i) the mixture is made too rich (lot of fuel compared to oxidizer) or too poor (too much oxidizer) such that the flame is close to its flammability limits (it cannot easily propagate); (ii) the feeding system and regions where the flame is not wanted are designed such that they impose strong heat loss to the flame in order to quench it. For a given thermodynamical state of the mixture (composition, temperature, pressure), the flame has its own dynamics (speed, heat release, etc) on which there is few control. On the other hand, those well defined quantities are convenient to describe the flame characteristics.
The Partially-Premixed Regime
This regime is somewhat less academics and has been recognized two decades ago. It is acknowledged as a hybrid of the premixed and the non-premixed regimes but the degree of interaction of these two modes of combustion to accurately describe a partially-premixed flame is still not well understood. It can be simply pictured by a lifted diffusion flame. Let us consider fuel issuing from a nozzle into the air. If the exit velocity is large enough, for some fuels, the flame lifts off the rim of the nozzle. It means that below the flame base, fuel and oxidizer have room to premix. Hence, the flame base propagates into a premixed mixture. However, it cannot be reduced to a premixed flame (although it is often simplified as this): (i) the mixing is not perfect and the different parts of the flame front constituting the flame base burn in mixtures of different thermodynamical states. This provides those parts with different deflagration capabilities such that the flame base has a complex shape. Indeed, it is convex, naturally leaded by the part burning at stoichiometry. (ii) Because the mixture is not homogeneous, transfer of species and temperature driven by diffusion occurs in a direction perpendicular to the propagation of the flame base. Because the flame front is not flat, those transfers act as a connection vehicle across the different parts of the leading front. (iii) The unburned left downstream by the sections of the leading front not burning at stoichiometry diffuse towards each other to form a diffusion flame as described above. The connection of the leading front with the trailing diffusion flame has been evidenced as complicated and the siege of transfers of species and temperature. These two last items are the state-of-the-art difficulties in understanding those flames and do not appear in the models although it has been demonstrated they have a major impact and are certainly a fundamental characteristic of partially-premixed flames.
Reaction mechanisms
Combustion is mainly a chemical process. Although we can, to some extent, describe a flame without any chemistry information, modelling of the flame propagation requires the knowledge of speeds of reactions, product concentrations, temperature, and other parameters. Therefore fundamental information about reaction kinetics is essential for any combustion model. A fuel-oxidizer mixture will generally combust if the reaction is fast enough to prevail until all of the mixture is burned into products. If the reaction is too slow, the flame will extinguish. If too fast, explosion or even detonation will occur. The reaction rate of a typical combustion reaction is influenced mainly by the concentration of the reactants, temperature, and pressure.
A stoichiometric equation for an arbitrary reaction can be written as:
|
|
where 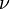 denotes the stoichiometric coefficient, and
denotes the stoichiometric coefficient, and 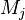 stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction.
stands for an arbitrary species. A one prime holds for the reactants while a double prime holds for the products of the reaction.
The reaction rate, expressing the rate of disappearance of reactant i, is defined as:
|
|
in which k is the specific reaction rate constant. Arrhenius found that this constant is a function of temperature only and is defined as:
|
|
where A is pre-exponential factor, E is the activation energy, and 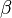 is a temperature exponent. The constants vary from one reaction to another and can be found in the literature.
is a temperature exponent. The constants vary from one reaction to another and can be found in the literature.
Reaction mechanisms can be deduced from experiments (for every resolved reaction), they can also be constructed numerically by the automatic generation method (see [Griffiths (1994)] for a review on reaction mechanisms). For simple hydrocarbons, tens to hundreds of reactions are involved. By analysis and systematic reduction of reaction mechanisms, global reactions (from one to five step reactions) can be found (see [Westbrook (1984)]).
Governing equations for chemically reacting flows
Together with the usual Navier-Stokes equations for compresible flow (See Governing equations), additional equations are needed in reacting flows.
The transport equation for the mass fraction 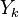 of k-th species is
of k-th species is
where Ficks' law is assumed for scalar diffusion with  denoting the species difussion coefficient, and
denoting the species difussion coefficient, and 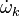 denoting the species reaction rate.
denoting the species reaction rate.
A non-reactive (passive) scalar (like the mixture fraction 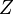 ) is goverened by the following transport equation
) is goverened by the following transport equation
where 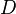 is the diffusion coefficient of the passive scalar.
is the diffusion coefficient of the passive scalar.
RANS equations
In turbulent flows, Favre averaging is often used to reduce the scales (see Reynolds averaging) and the mass fraction transport equation is transformed to
where the turbulent fluxes 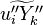 and reaction terms
and reaction terms
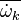 need to be closed.
need to be closed.
The passive scalar turbulent transport equation is
where 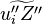 needs modelling. A common practice is to model the turbulent fluxes using the
gradient diffusion hypothesis. For example, in the equation above the flux
needs modelling. A common practice is to model the turbulent fluxes using the
gradient diffusion hypothesis. For example, in the equation above the flux 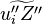 is modelled as
is modelled as
where 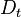 is the turbulent diffusivity. Since
is the turbulent diffusivity. Since 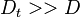 , the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.
, the first term inside the parentheses on the right hand of the mixture fraction transport equation is often neglected (Peters (2000)). This assumption is also used below.
In addition to the mean passive scalar equation,
an equation for the Favre variance 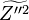 is often employed
is often employed
where 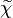 is the mean Scalar dissipation rate
defined as
is the mean Scalar dissipation rate
defined as 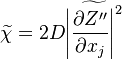 This term and the variance diffusion fluxes needs to be modelled.
This term and the variance diffusion fluxes needs to be modelled.
LES equations
The Large eddy simulation (LES) approach for reactive flows introduces equations for the filtered species mass fractions within the compressible flow field. Similar to the #RANS equations, but using Favre filtering instead of Favre averaging, the filtered mass fraction transport equation is
where 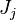 is the transport of subgrid fluctuations of mass fraction
is the transport of subgrid fluctuations of mass fraction
and has to be modelled.
Fluctuations of diffusion coefficients are often ignored and their contributions are assumed to be much smaller than the apparent turbulent diffusion due to transport of subgrid fluctuations. The first term on the right hand side is then
Infinitely fast chemistry
All combustion models can be divided into two main groups according to the assumptions on the reaction kinetics. We can either assume the reactions to be infinitely fast - compared to e.g. mixing of the species, or comparable to the time scale of the mixing process. The simple approach is to assume infinitely fast chemistry. Historically, mixing of the species is the older approach, and it is still in wide use today. It is therefore simpler to solve for #Finite rate chemistry models, at the overshoot of introducing errors to the solution.
Premixed combustion
Premixed flames occur when the fuel and oxidiser are homogeneously mixed prior to ignition. These flames are not limited only to gas fuels, but also to the pre-vaporised fuels. Typical examples of premixed laminar flames is bunsen burner, where the air enters the fuel stream and the mixture burns in the wake of the riser tube walls forming nice stable flame. Another example of a premixed system is the solid rocket motor where oxidizer and fuel and properly mixed in a gum-like matrix that is uniformly distributed on the periphery of the chamber. Premixed flames have many advantages in terms of control of temperature and products and pollution concentration. However, they introduce some dangers like the autoignition (in the supply system).
Turbulent flame speed model
Eddy Break-Up model
The Eddy Break-Up model is the typical example of mixed-is-burnt combustion model. It is based on the work of Magnussen, Hjertager, and Spalding and can be found in all commercial CFD packages. The model assumes that the reactions are completed at the moment of mixing, so that the reaction rate is completely controlled by turbulent mixing. Combustion is then described by a single step global chemical reaction
|
|
in which F stands for fuel, O for oxidiser, and P for products of the reaction. Alternativelly we can have a multistep scheme, where each reaction has its own mean reaction rate. The mean reaction rate is given by
|
|
where 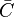 denotes the mean concentrations of fuel, oxidiser, and products
respectively. A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for all the situations. Care must be taken especially in highly strained regions, where the ratio of
denotes the mean concentrations of fuel, oxidiser, and products
respectively. A and B are model constants with typical values of 0.5
and 4.0 respectively. The values of these constants are fitted according
to experimental results and they are suitable for most cases of general interest. It is important to note that these constants are only based on experimental fitting and they need not be suitable for all the situations. Care must be taken especially in highly strained regions, where the ratio of  to
to  is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually have some remedies to overcome this problem.
is large (flame-holder wakes, walls ...). In these, regions a positive reaction rate occurs and an artificial flame can be observed.
CFD codes usually have some remedies to overcome this problem.
This model largely over-predicts temperatures and concentrations of species like CO and other species. However, the Eddy Break-Up model enjoys a popularity for its simplicity, steady convergence, and implementation.
Bray-Moss-Libby model
Non-premixed combustion
Non premixed combustion is a special class of combustion where fuel and oxidizer
enter separately into the combustion chamber. The diffusion and mixing of the two streams
must bring the reactants together for the reaction to occur.
Mixing becomes the key characteristic for diffusion flames.
Diffusion burners are easier and safer to operate than premixed burners.
However their efficiency is reduced compared to premixed burners.
One of the major theoretical tools in non-premixed combustion
is the passive scalar mixture fraction 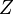 which is the
backbone on most of the numerical methods in non-premixed combustion.
which is the
backbone on most of the numerical methods in non-premixed combustion.
Conserved scalar equilibrium models
The reactive problem is split into two parts. First, the problem of mixing , which consists of the location of the flame surface which is a non-reactive problem concerning the propagation of a passive scalar; And second, the flame structure problem, which deals with the distribution of the reactive species inside the flamelet.
To obtain the distribution inside the flame front we assume it is locally one-dimensional and depends only on time and the scalar coodinate.
We first make use of the following chain rules
and transformation
upon substitution into the species transport equation (see #Governing Equations for Reacting Flows), we obtain
The second and third terms in the LHS cancel out due to continuity and mixture fraction transport. At the outset, the equation boils down to
where 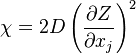 is called the scalar dissipation
which controls the mixing, providing the interaction between the flow and the chemistry.
is called the scalar dissipation
which controls the mixing, providing the interaction between the flow and the chemistry.
If the flame dependence on time is dropped, even though the field  still depends on it.
still depends on it.
If the reaction is assumed to be infinetly fast, the resultant flame distribution is in equilibrium.
and 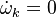 . When the flame is in equilibrium, the flame configuration
. When the flame is in equilibrium, the flame configuration 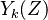 is independent of strain.
is independent of strain.
Burke-Schumann flame structure
The Burke-Schuman solution is valid for irreversible infinitely fast chemistry. With a reaction in the form of
|
|
If the flame is in equilibrium and therefore the reaction term is 0.
Two possible solution exists, one with pure mixing (no reaction)
and a linear dependence of the species mass fraction with 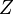 .
Fuel mass fraction
.
Fuel mass fraction
Oxidizer mass fraction
Where 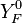 and
and 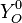 are fuel and oxidizer mass fractions
in the pure fuel and oxidizer streams respectively.
are fuel and oxidizer mass fractions
in the pure fuel and oxidizer streams respectively.
The other solution is given by a discontinuous slope at stoichiometric mixture fraction
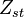 and two linear profiles (in the rich and lean side) at either
side of the stoichiometric mixture fraction.
Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.
and two linear profiles (in the rich and lean side) at either
side of the stoichiometric mixture fraction.
Both concentrations must be 0 at stoichiometric, the reactants become products infinitely fast.
and oxidizer mass fraction
Finite rate chemistry
Premixed combustion
Coherent flame model
Flamelets based on G-equation
Flame surface density model
Non-premixed combustion
Flamelets based on conserved scalar
Peters (2000) define Flamelets as "thin diffusion layers embedded in a turbulent non-reactive flow field".
If the chemistry is fast enough, the chemistry is active within a thin region
where the chemistry conditions are in (or close to) stoichiometric conditions, the "flame" surface.
This thin region is assumed to be smaller than Kolmogorov length scale and therefore the
region is locally laminar. The flame surface is defined as an iso-surface of a certain scalar 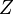 ,
mixture fraction in #Non premixed combustion.
,
mixture fraction in #Non premixed combustion.
The same equation used in #Conserved scalar models for equilibrium chemistry is used here but with chemical source term different from 0
This approach is called the Stationary Laminar Flamelet Model (SLFM) and has the advantage that
flamelet profiles 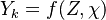 can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.
For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory COSILAB [1] with its relevant solver RUN1DL, which can be used for a variety of relevant geometries; see various publications that are available for download. Other software tools are available such as CHEMKIN [2] and
CANTERA [3].
can be pre-computed and stored in a dtaset or file which is called a "flamelet library" with all the required complex chemistry.
For the generation of such libraries ready to use software is avalable such as Softpredict's Combustion Simulation Laboratory COSILAB [1] with its relevant solver RUN1DL, which can be used for a variety of relevant geometries; see various publications that are available for download. Other software tools are available such as CHEMKIN [2] and
CANTERA [3].
Flamelets in turbulent combustion
In turbulent flames the interest is 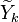 .
In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scale
and obviously is much smaller than the grid size.
It is therefore needed a distribution of the passive scalar within the cell.
.
In flamelets, the flame thickness is assumed to be much smaller than Kolmogorov scale
and obviously is much smaller than the grid size.
It is therefore needed a distribution of the passive scalar within the cell.
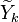 cannot be obtained directly from the flamelets library
cannot be obtained directly from the flamelets library
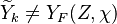 , where
, where 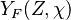 corresponds
to the value obtained from the flamelets libraries.
A generic solution can be expressed as
corresponds
to the value obtained from the flamelets libraries.
A generic solution can be expressed as
where 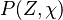 is the joint Probability Density Function (PDF) of the mixture fraction
and scalar dissipation which account for the scalar distribution inside the cell and "a priori"
depends on time and space.
is the joint Probability Density Function (PDF) of the mixture fraction
and scalar dissipation which account for the scalar distribution inside the cell and "a priori"
depends on time and space.
The most simple assumption is to use a constant distribution of the scalar dissipation within the cell and the above equation reduces to
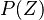 is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a beta PDF)
can be build depending only on two moments of the scalar
mean and variance,
is the PDF of the mixture fraction scalar and simple models (such as Gaussian or a beta PDF)
can be build depending only on two moments of the scalar
mean and variance,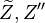 .
.
If the mixture fraction and scalar dissipation are consider independent variables,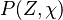 can be written as
can be written as 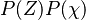 . The PDF of the scalar dissipation is assumed to be log-normal with
variance unity.
. The PDF of the scalar dissipation is assumed to be log-normal with
variance unity.
In Large eddy simulation (LES) context (see #LES equations for reacting flow),
the probability density function is replaced by a subgrid PDF 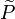 .
The same equation hold by replacing averaged values with filtered values.
.
The same equation hold by replacing averaged values with filtered values.
The assumptions made regarding the shapes of the PDFs are still justified. In LES combustion the subgrid variance is smaller than RANS counterpart (part of the large-scale fluctuations are solved) and therefore the modelled PDFs are thinner.
Unsteady flamelets
Intrinsic Low Dimensional Manifolds (ILDM)
Detailed mechanisms describing ignition, flame propagation and pollutant formation typically involve several hundred species and elementary reactions, prohibiting their use in practical three-dimensional engine simulations. Conventionally reduced mechanisms often fail to predict minor radicals and pollutant precursors. The ILDM-method is an automatic reduction of a detailed mechanism, which assumes local equilibrium with respect to the fastest time scales identified by a local eigenvector analysis. In the reactive flow calculation, the species compositions are constrained to these manifolds. Conservation equations are solved for only a small number of reaction progress variables, thereby retaining the accuracy of detailed chemical mechanisms. This gives an effective way of coupling the details of complex chemistry with the time variations due to turbulence.
The intrinsic low-dimensional manifold (ILDM) method {Maas:1992,Maas:1993} is a method for in-situ reduction of a detailed chemical mechanism based on a local time scale analysis. This method is based on the fact that different trajectories in state space start from a high-dimensional point and quickly relax to lower-dimensional manifolds due to the fast reactions. The movement along these lower-dimensional manifolds, however, is governed by the slow reactions. It exploits the variety of time scales to systematically reduce the detailed mechanism. For a detailed chemical mechanism with N species, N different time scales govern the process. An assumption that all the time scales are relaxed results in assuming complete equilibrium, where the only variables required to describe the system are the mixture fraction, the temperature and the pressure. This results in a zero-dimensional manifold. An assumption that all but the slowest 'n' time scales are relaxed results in a 'n' dimensional manifold, which requires the additional specification of 'n' parameters (called progress variables). In the ILDM method, the fast chemical reactions do not need to be identified a priori. An eigenvalue analysis of the detailed chemical mechanism is carried out which identifies the fast processes in dynamic equilibrium with the slow processes. The computation of ILDM points can be expensive, and hence an in-situ tabulation procedure is used, which enables the calculation of only those points that are needed during the CFD calculation.
--Fredgauss 07:37, 25 August 2006 (MDT)
U. Maas, S.B. Pope. Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space. Comb. Flame 88, 239, 1992.
Ulrich Maas. Automatische Reduktion von Reaktionsmechanismen zur Simulation reaktiver Str¨omungen. Habilitationsschrift, Universit ¨at Stuttgart, 1993.
Conditional Moment Closure (CMC)
In Conditional Moment Closure (CMC) methods we assume that the species mass fractions are all correlated with the mixture fraction (in non premixed combustion).
From Probability density function we have
where 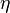 is the sample space for
is the sample space for 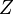 .
.
CMC consists of providing a set of transport equations for the conditional moments which define the flame structure.
Experimentally, it has been observed that temperature and chemical radicals are strong non-linear functions of mixture fraction. For a given species mass fraction we can decomposed it into a mean and a fluctuation:
The fluctuations 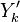 are usually very strong in time and space which makes the closure
of
are usually very strong in time and space which makes the closure
of 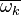 very difficult.
However, the alternative decomposition
very difficult.
However, the alternative decomposition
where 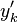 is the fluctuation around the conditional mean or the "conditional fluctuation".
Experimentally, it is observed that
is the fluctuation around the conditional mean or the "conditional fluctuation".
Experimentally, it is observed that 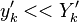 , which forms the basic assumption of the CMC method.
Closures. Due to this property better closure methods can be used reducing the non-linearity
of the mass fraction equations.
, which forms the basic assumption of the CMC method.
Closures. Due to this property better closure methods can be used reducing the non-linearity
of the mass fraction equations.
The Derivation of the CMC equations produces the following CMC transport equation
where 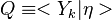 for simplicity.
for simplicity.
In this equation, high order terms in Reynolds number have been neglected. (See Derivation of the CMC equations for the complete series of terms).
It is well known that closure of the unconditional source term
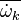 as a function of the
mean temperature and species (
as a function of the
mean temperature and species (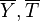 ) will give rise to large errors.
However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.
The first order closure
) will give rise to large errors.
However, in CMC the conditional averaged mass fractions contain more information and fluctuations around the mean are much smaller.
The first order closure
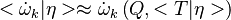 is a good approximation in zones which are not close to extinction.
is a good approximation in zones which are not close to extinction.
Second order closure
A second order closure can be obtained if conditional fluctuations are taken into account.
For a chemical source term in the form 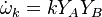 with the rate constant in Arrhenius form
with the rate constant in Arrhenius form
![k=A_0 T^\beta exp [-Ta/T]](/W/images/math/2/e/0/2e0c186caff5787cd5f2f76baac86531.png) the second order closure is (Klimenko and Bilger 1999)
the second order closure is (Klimenko and Bilger 1999)
where 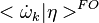 is the first order CMC closure and
is the first order CMC closure and
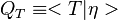 .
When the temperature exponent
.
When the temperature exponent 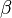 or
or 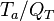 are large the error of taking the first order approximation increases.
Improvement of small pollutant predictions can be obtained using the above reaction
rate for selected species like CO and NO.
are large the error of taking the first order approximation increases.
Improvement of small pollutant predictions can be obtained using the above reaction
rate for selected species like CO and NO.
Double conditioning
Close to extinction and reignition. The conditional fluctuations can be very large
and the primary closure of CMC of "small" fluctuations is not longer valid.
A second variable 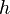 can be chosen to define a double conditioned mass fraction
can be chosen to define a double conditioned mass fraction
Due to the strong dependence on chemical reactions to temperature, 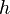 is advised to be a temperature related variable (Kronenburg 2004).
Scalar dissipation is not a good choice, due to its log-normal behaviour
(smaller scales give highest dissipation). A must better choice is the sensible enthalpy
or a progress variable.
Double conditional variables have much smaller conditional fluctuations and allow
the existence of points with the same chemical composition which can be fully burning
(high temperature) or just mixing (low temperature).
The range of applicability is greatly increased and allows non-premixed and premixed problems
to be treated without ad-hoc distinctions.
The main problem is the closure of the new terms involving cross scalar transport.
is advised to be a temperature related variable (Kronenburg 2004).
Scalar dissipation is not a good choice, due to its log-normal behaviour
(smaller scales give highest dissipation). A must better choice is the sensible enthalpy
or a progress variable.
Double conditional variables have much smaller conditional fluctuations and allow
the existence of points with the same chemical composition which can be fully burning
(high temperature) or just mixing (low temperature).
The range of applicability is greatly increased and allows non-premixed and premixed problems
to be treated without ad-hoc distinctions.
The main problem is the closure of the new terms involving cross scalar transport.
The double conditional CMC equation is obtained in a similar manner than the conventional CMC equations
LES modelling
In a LES context a conditional filtering operator can be defined
and 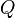 therefore represents a conditionally filtered reactive scalar.
therefore represents a conditionally filtered reactive scalar.
Linear Eddy Model
The Linear Eddy Model (LEM) was first developed by Kerstein(1988). It is an one-dimensional model for representing the flame structure in turbulent flows.
In every computational cell a molecular, diffusion and chemical model is defined as
where 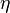 is a spatial coordinate. The scalar distribution obtained can be seen as a
one-dimensional reference field between Kolmogorov scale and grid scales.
is a spatial coordinate. The scalar distribution obtained can be seen as a
one-dimensional reference field between Kolmogorov scale and grid scales.
In a second stage a series of re-arranging stochastic event take place.
These events represent the effects
of a certain turbulent structure of size 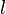 , smaller than the grid size at a location
, smaller than the grid size at a location 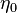 within the one-dimensional domain. This vortex distort the
within the one-dimensional domain. This vortex distort the 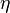 field obtain by the one-dimensional equation,
creating new maxima and minima in the interval
field obtain by the one-dimensional equation,
creating new maxima and minima in the interval 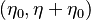 .
The vortex size
.
The vortex size 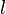 is chosen randomly based on the inertial scale range while
is chosen randomly based on the inertial scale range while
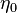 is obtained from a uniform distribution in
is obtained from a uniform distribution in 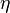 .
The number of events is chosen to match the turbulent diffusivity of the flow.
.
The number of events is chosen to match the turbulent diffusivity of the flow.
PDF transport models
Probability Density Function (PDF) methods are not exclusive to combustion, although they are particularly attractive to them. They provided more information than moment closures and they are used to compute inhomegenous turbulent flows, see reviews in Dopazo (1993) and Pope (1994).
PDF methods are based on the transport equation of the joint-PDF of the scalars.
Denoting 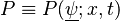 where
where
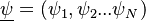 is the phase space for the reactive scalars
is the phase space for the reactive scalars
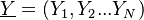 .
The transport equation of the joint PDF is:
.
The transport equation of the joint PDF is:
where the chemical source term is closed. Another term appeared on the right hand side which accounts for the effects of
the molecular mixing on the PDF, is the so called "micro-mixing " term.
Equal diffusivities are used for simplicity 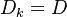
A more general approach is the velocity-composition joint-PDF
with 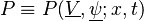 , where
, where
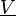 is the sample space of the velocity field
is the sample space of the velocity field
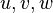 . This approach has the advantage of avoiding gradient-diffusion
modelling. A similar equation to the above is obtained combining the momentum
and scalar transport equation.
. This approach has the advantage of avoiding gradient-diffusion
modelling. A similar equation to the above is obtained combining the momentum
and scalar transport equation.
The PDF transport equation can be solved in two ways: through a Lagrangian approach
using stochastic methods or in a Eulerian ways using stochastic fields.
Lagrangian
The main idea of Lagrangian methods is that the flow can be represented by an ensemble of fluid particles. Central to this approach is the stochastic differential equations and in particular the Langevin equation.
Eulerian
Instead of stochastic particles, smooth stochastic fields can be used to represent the probability density function (PDF) of a scalar (or joint PDF) involved in transport (convection), diffusion and chemical reaction (Valino 1998). A similar formulation was proposed by Sabelnikov and Soulard 2005, which removes part of the a-priori assumption of "smoothness" of the stochastic fields. This approach is purely Eulerian and offers implementations advantages compared to Lagrangian or semi-Eulerian methods. Transport equations for scalars are often easy to programme and normal CFD algorithms can be used (see Discretisation of convective term). Although discretization errors are introduced by solving transport equations, this is partially compesated by the error introduced in Lagrangian approaches due to the numerical evaluation of means.
A new set of 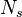 scalar variables
(the stochastic field
scalar variables
(the stochastic field 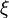 ) is used to represent the
PDF
) is used to represent the
PDF
Other combustion models
MMC
The Multiple Mapping Conditioning (MMC) (Klimenko and Pope 2003) is an extension of the #Conditional Moment Closure (CMC) approach combined with probability density function methods. MMC looks for the minimum set of variables that describes the particular turbulent combustion system.
Fractals
Derived from the #Eddy Dissipation Concept (EDC).
References
- Dopazo, C. (1993), "Recent development in PDF methods", Turbulent Reacting Flows, ed. P. A. Libby and F. A. Williams.
- Fox, R.O. (2003), Computational Models for Turbulent Reacting Flows, ISBN 0-521-65049-6,Cambridge University Press.
- Kerstein, A. R. (1988), "A linear eddy model of turbulent scalar transport and mixing", Comb. Science and Technology, Vol. 60,pp. 391.
- Klimenko, A. Y., Bilger, R. W. (1999), "Conditional moment closure for turbulent combustion", Progress in Energy and Combustion Science, Vol. 25,pp. 595-687.
- Klimenko, A. Y., Pope, S. B. (2003), "The modeling of turbulent reactive flows based on multiple mapping conditioning", Physics of Fluids, Vol. 15, Num. 7, pp. 1907-1925.
- Kronenburg, A., (2004), "Double conditioning of reactive scalar transport equations in turbulent non-premixed flames", Physics of Fluids, Vol. 16, Num. 7, pp. 2640-2648.
- Griffiths, J. F. (1994), "Reduced Kinetic Models and Their Application to Practical Combustion Systems", Prog. in Energy and Combustion Science,Vol. 21, pp. 25-107.
- Peters, N. (2000), Turbulent Combustion, ISBN 0-521-66082-3,Cambridge University Press.
- Poinsot, T.,Veynante, D. (2001), Theoretical and Numerical Combustion, ISBN 1-930217-05-6, R. T Edwards.
- Pope, S. B. (1994), "Lagrangian PDF methods for turbulent flows", Annu. Rev. Fluid Mech, Vol. 26, pp. 23-63.
- Sabel'nikov, V.,Soulard, O. (2005), "Rapidly decorrelating velocity-field model as a tool for solving one-point Fokker-Planck equations for probability density functions of turbulent reactive scalars", Physical Review E, Vol. 72,pp. 016301-1-22.
- Valino, L., (1998), "A field montecarlo formulation for calculating the probability density function of a single scalar in a turbulent flow", Flow. Turb and Combustion, Vol. 60,pp. 157-172.
- Westbrook, Ch. K., Dryer,F. L., (1984), "Chemical Kinetic Modeling of Hydrocarbon Combustion", Prog. in Energy and Combustion Science,Vol. 10, pp. 1-57.

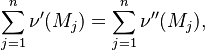
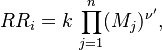
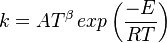
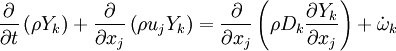
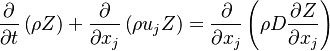
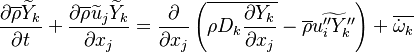
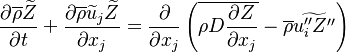
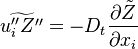
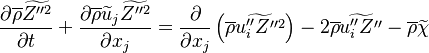
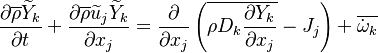
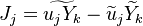
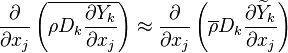
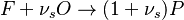
![\bar{\dot\omega}_F=A_{EB} \frac{\epsilon}{k}
min\left[\bar{C}_F,\frac{\bar{C}_O}{\nu},
B_{EB}\frac{\bar{C}_P}{(1+\nu)}\right]](/W/images/math/9/d/6/9d67c48a8dd1f2decb0d5bf3336d215b.png)
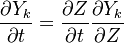
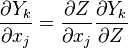
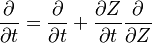
![\rho \frac{\partial Y_k}{\partial t} + Y_k \left[
\frac{\partial \rho}{\partial t} + \frac{\partial \rho u_j}{\partial x_j}
\right]
+ \frac{\partial Y_k}{\partial Z} \left[
\rho \frac{\partial Z}{\partial t} + \rho u_j \frac{\partial Z}{\partial x_j} -
\frac{\partial}{\partial x_j}\left( \rho D \frac{\partial Z}{\partial x_j} \right)
\right]
=
\rho D \left( \frac{\partial Z}{\partial x_j} \frac{\partial Z}{\partial x_j} \right)
\frac{\partial^2 Y_k}{\partial Z^2} + \dot \omega_k](/W/images/math/7/6/9/76972aa831910042bbf0ce5e9610a31b.png)
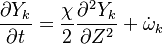
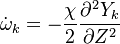
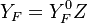
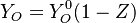
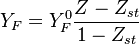
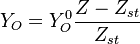

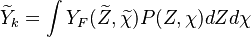
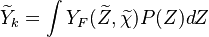
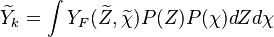
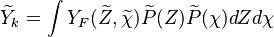
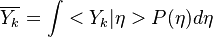
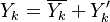
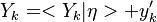
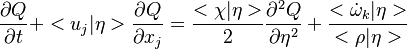
![< \dot \omega_k|\eta> \approx < \dot \omega_k|\eta >^{FO}
\left[1+ \frac{< Y''_A Y''_B |\eta>}{Q_A Q_B}+ \left( \beta + T_a/Q_T \right)
\left(
\frac{< Y''_A T'' |\eta>}{Q_AQ_T} + \frac{< Y''_B T'' |\eta>}{Q_BQ_T}
\right) + ...
\right]](/W/images/math/f/9/c/f9c779360789a63c6bb68e8c13d0489a.png)
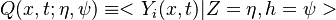
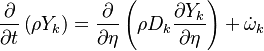
![\frac{\partial <\rho | \underline{Y}=\underline{\psi}> P }{\partial t} + \frac{
\partial <\rho u_j | \underline{Y}=\underline{\psi}> P }{\partial x_j} =
\sum^N_\alpha \frac{\partial}{\partial \psi_\alpha}\left[ \rho \dot{\omega}_\alpha P \right]
- \sum^N_\alpha \sum^N_\beta \frac{\partial^2}{\partial \psi_\alpha \psi_\beta}
\left[ <D \frac{\partial Y_\alpha}{\partial x_i} \frac{\partial Y_\beta}{\partial x_i} | \underline{Y}=\underline{\psi}> \right] P](/W/images/math/1/3/7/13767f4c5947b8df82fdd84c944ea62b.png)
![P (\underline{\psi}; x,t) = \frac{1}{N} \sum^{N_s}_{j=1} \prod^{N}_{k=1} \delta \left[\psi_k -\xi_k^j(x,t) \right]](/W/images/math/f/2/3/f23f3d712f59f83ab17babbfbe9834ab.png)