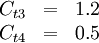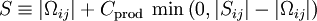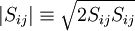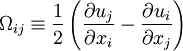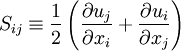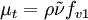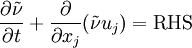Spalart-Allmaras model
From CFD-Wiki
(split a long equation into two lines) |
|||
| Line 10: | Line 10: | ||
:<math> | :<math> | ||
| - | \frac{\partial \tilde{\nu}}{\partial t} + u_j \frac{\partial \tilde{\nu}}{\partial x_j} = C_{b1} [1 - f_{t2}] \tilde{S} \tilde{\nu} + \frac{1}{\sigma} \{ \nabla \cdot [(\nu + \tilde{\nu}) \nabla \tilde{\nu}] + C_{b2} | \nabla \nu |^2 \} - \left[C_{w1} f_w - \frac{C_{b1}}{\kappa^2} f_{t2}\right] \left( \frac{\tilde{\nu}}{d} \right)^2 + f_{t1} \Delta U^2 | + | \begin{matrix} |
| + | \frac{\partial \tilde{\nu}}{\partial t} + u_j \frac{\partial \tilde{\nu}}{\partial x_j} & = & C_{b1} [1 - f_{t2}] \tilde{S} \tilde{\nu} + \frac{1}{\sigma} \{ \nabla \cdot [(\nu + \tilde{\nu}) \nabla \tilde{\nu}] + C_{b2} | \nabla \nu |^2 \} - \\ | ||
| + | \ & \ & \left[C_{w1} f_w - \frac{C_{b1}}{\kappa^2} f_{t2}\right] \left( \frac{\tilde{\nu}}{d} \right)^2 + f_{t1} \Delta U^2 \\ | ||
| + | \end{matrix} | ||
</math> | </math> | ||
Revision as of 09:34, 12 June 2007
Spalart-Allmaras model is a one equation model for the turbulent viscosity.
Contents |
Original model
The turbulent eddy viscosity is given by
where
- d is the distance to the closest surface
The constants are
Modifications to original model
According to Spalart it is safer to use the following values for the last two constants:
[Dacles-Mariani et. al. 1995] proposed a modification of the model which also accounts for the effect of mean strain rate on turbulence production. This modification instead prescribes:
where
Other models related to the S-A model:
DES (1999) [1]
DDES (2006)
Model for compressible flows
There are two approaches to adapting the model for compressible flows. In the first approach the turbulent dynamic viscosity is computed from
where 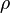 is the local density. The convective terms in the equation for
is the local density. The convective terms in the equation for 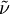 are modified to
are modified to
where the right hand side (RHS) is the same as in the original model.
Boundary conditions
Walls: 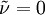
Freestream: Ideally 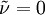 , but some solvers can have problem with that so
, but some solvers can have problem with that so 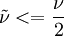 can be used. This is if the trip term is used to "start up" the model. A convenient option is to set
can be used. This is if the trip term is used to "start up" the model. A convenient option is to set  in the freestream. The model then provides fully turbulent results and any regions like boundary layers that contain shear become fully turbulent.
in the freestream. The model then provides fully turbulent results and any regions like boundary layers that contain shear become fully turbulent.
Outlet: convective outlet.
References
- Dacles-Mariani, J., Zilliac, G. G., Chow, J. S. and Bradshaw, P. (1995), "Numerical/Experimental Study of a Wingtip Vortex in the Near Field", AIAA Journal, 33(9), pp. 1561-1568, 1995.
- Spalart, P. R. and Allmaras, S. R. (1992), "A One-Equation Turbulence Model for Aerodynamic Flows", AIAA Paper 92-0439.
- Spalart, P. R. and Allmaras, S. R. (1994), "A One-Equation Turbulence Model for Aerodynamic Flows", La Recherche Aerospatiale n 1, 5-21.

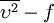 model
model
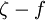 model
model

![\begin{matrix}
\frac{\partial \tilde{\nu}}{\partial t} + u_j \frac{\partial \tilde{\nu}}{\partial x_j} & = & C_{b1} [1 - f_{t2}] \tilde{S} \tilde{\nu} + \frac{1}{\sigma} \{ \nabla \cdot [(\nu + \tilde{\nu}) \nabla \tilde{\nu}] + C_{b2} | \nabla \nu |^2 \} - \\
\ & \ & \left[C_{w1} f_w - \frac{C_{b1}}{\kappa^2} f_{t2}\right] \left( \frac{\tilde{\nu}}{d} \right)^2 + f_{t1} \Delta U^2 \\
\end{matrix}](/W/images/math/6/8/6/6862e971bbdc4ecba669c49b9d5fc2ee.png)
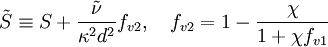
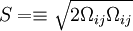

![f_w = g \left[ \frac{ 1 + C_{w3}^6 }{ g^6 + C_{w3}^6 } \right]^{1/6}, \quad g = r + C_{w2}(r^6 - r), \quad r \equiv \frac{\tilde{\nu} }{ \tilde{S} \kappa^2 d^2 }](/W/images/math/0/9/b/09b19885ed6dffe3dec850e2516f1696.png)
![f_{t1} = C_{t1} g_t \exp\left( -C_{t2} \frac{\omega_t^2}{\Delta U^2} [ d^2 + g^2_t d^2_t] \right)](/W/images/math/9/9/3/993b41d0ba795e0b3877d041c4cff1cb.png)