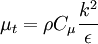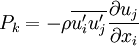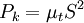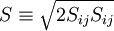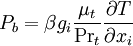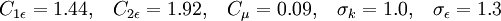Standard k-epsilon model
From CFD-Wiki
(Difference between revisions)
(Added section "References", pointing to the section of the same name on the parent page) |
(Someone added that C3 was -0.33, without any reference. This can be confusing to OpenFOAM users, because their k-epsilon has another C3, for another reason.) |
||
| Line 51: | Line 51: | ||
:<math> | :<math> | ||
| - | C_{1 \epsilon} = 1.44, \;\;\; C_{2 \epsilon} = 1.92 | + | C_{1 \epsilon} = 1.44, \;\;\; C_{2 \epsilon} = 1.92,\;\; \; C_{\mu} = 0.09, \;\;\; \sigma_k = 1.0, \;\;\; \sigma_{\epsilon} = 1.3 |
</math> | </math> | ||
| + | |||
| + | |||
| + | '''Note''': <math>C_{3 \epsilon}</math> depends on the literature being followed and is meant to be used only with the <math>P_b</math> term. Possible values, depending on literature reference: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- align="center" | ||
| + | ! Reference !! Constant !! Comments | ||
| + | |- align="center" | ||
| + | | ''unknown'' || <math>C_{3 \epsilon} = -0.33</math> || Note to OpenFOAM users: do not confuse this constant with the one used in their implementations of the k-epsilon turbulence models. Their implementation is different. | ||
| + | |} | ||
Latest revision as of 20:15, 16 December 2014
Contents |
Transport equations for standard k-epsilon model
For turbulent kinetic energy 
For dissipation 
Modeling turbulent viscosity
Turbulent viscosity is modelled as:
Production of k
Where  is the modulus of the mean rate-of-strain tensor, defined as :
is the modulus of the mean rate-of-strain tensor, defined as :
Effect of buoyancy
where Prt is the turbulent Prandtl number for energy and gi is the component of the gravitational vector in the ith direction. For the standard and realizable - models, the default value of Prt is 0.85.
The coefficient of thermal expansion, 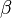 , is defined as
, is defined as
Model constants
Note: 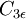 depends on the literature being followed and is meant to be used only with the
depends on the literature being followed and is meant to be used only with the 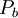 term. Possible values, depending on literature reference:
term. Possible values, depending on literature reference:
| Reference | Constant | Comments |
|---|---|---|
| unknown | 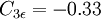 | Note to OpenFOAM users: do not confuse this constant with the one used in their implementations of the k-epsilon turbulence models. Their implementation is different. |
References
See section References in the parent page K-epsilon models.

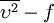 model
model
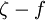 model
model
![\frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k](/W/images/math/0/3/3/03313e8802538459d0a202c34efc1274.png)
![\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left[\left(\mu + \frac{\mu_t}{\sigma_{\epsilon}} \right) \frac{\partial \epsilon}{\partial x_j} \right] + C_{1 \epsilon}\frac{\epsilon}{k} \left( P_k + C_{3 \epsilon} P_b \right) - C_{2 \epsilon} \rho \frac{\epsilon^2}{k} + S_{\epsilon}](/W/images/math/0/6/c/06ca9efd2f29b3816707de0452572c77.png)