Near-wall treatment for k-omega models
From CFD-Wiki
(the formula for kp is wrong) |
|||
| (10 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
{{Turbulence modeling}} | {{Turbulence modeling}} | ||
| - | ==Standard wall | + | As described in [[Two equation turbulence models]] low and high reynolds number treatments are possible. |
| - | + | ==Standard wall functions== | |
| - | + | Main page: [[Two equation models#Near-wall treatments| Two equation near-wall treatments]] | |
| - | + | ||
| - | + | For <math>k</math> the boundary conditions imposed at the solid boundary are: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | <math> | + | |
| - | + | ||
| - | </math> | + | |
| - | + | ||
:<math> | :<math> | ||
| - | + | \begin{matrix} | |
| + | \frac{\partial k}{\partial n} = 0 & & \frac{\partial \omega}{\partial n} = 0 | ||
| + | \end{matrix} | ||
</math> | </math> | ||
| - | + | where <math>n</math> is the normal to the boundary. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Moreover the centroid values in cells adjacent to solid wall are specified as | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
:<math> | :<math> | ||
| - | + | \begin{matrix} | |
| + | k_p = \frac{u^2_\tau}{\sqrt{C_\mu}}, | ||
| + | && | ||
| + | \omega_p = \frac{u_\tau}{\sqrt{C_\mu}\kappa y_p} = \frac{\sqrt{k_p}}{{C_\mu^{1/4}}\kappa y_p}. | ||
| + | \end{matrix} | ||
</math> | </math> | ||
| - | + | In the alternative approach <math>k</math> production terms is modified. | |
| + | ==Automatic wall treatments== | ||
| + | The purpose of automatic wall treatments is to make results insensitive with respect to wall mesh refinement. Many blending approaches have been proposed. The one by Menter takes advantage of the fact that the solution to <math>\omega</math> equations is known for both viscous and log layer | ||
:<math> | :<math> | ||
| - | + | \begin{matrix} | |
| + | \omega_\text{vis} = \frac{6\nu}{\beta y^2} & \omega_\text{log} = \frac{u_\tau}{C_\mu^{1/4} \kappa y} | ||
| + | \end{matrix} | ||
</math> | </math> | ||
| + | where <math>y</math> is the cell centroid distance from the wall. Using this a blending can take the following form: | ||
:<math> | :<math> | ||
| - | \omega_p = \ | + | \omega_p = \sqrt{\omega_{\text{vis}}^2 + \omega_{\text{log}}^2}, |
</math> | </math> | ||
| - | + | Note that for low <math>y</math> values the <math>1/y^2</math> will dominate and therefore viscous value of <math>\omega</math> will be reproduced. Conversely, for larger values of <math>y</math>, <math>1/y</math> will be dominant and logarithmic value will be recovered. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | Subsequently Menter proposes also blending for friction velocity. Friction velocity for viscous and logarithmic region are: | ||
:<math> | :<math> | ||
| - | + | \begin{matrix} | |
| + | u^\text{vis}_\tau = \frac{U}{y^{+}} & & u_\tau^\text{log} = \frac{U}{\log E y^{+}} | ||
| + | \end{matrix} | ||
</math> | </math> | ||
| - | + | And the blending suggested: | |
| - | : | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
:<math> | :<math> | ||
u_\tau = \sqrt[4]{(u_\tau^{\text{vis}})^4 + (u_\tau^{\text{log}})^4}, | u_\tau = \sqrt[4]{(u_\tau^{\text{vis}})^4 + (u_\tau^{\text{log}})^4}, | ||
| Line 91: | Line 66: | ||
== References == | == References == | ||
| - | |||
| - | |||
* {{reference-paper|author=Menter, F., Esch, T.|year=2001|title=Elements of industrial heat transfer predictions|rest='COBEM 2001, 16th Brazilian Congress of Mechanical Engineering.'}} | * {{reference-paper|author=Menter, F., Esch, T.|year=2001|title=Elements of industrial heat transfer predictions|rest='COBEM 2001, 16th Brazilian Congress of Mechanical Engineering.'}} | ||
* {{reference-paper|author=ANSYS|year=2006|title=FLUENT Documentation|rest=''}} | * {{reference-paper|author=ANSYS|year=2006|title=FLUENT Documentation|rest=''}} | ||
Latest revision as of 10:40, 31 March 2021
As described in Two equation turbulence models low and high reynolds number treatments are possible.
Contents |
Standard wall functions
Main page: Two equation near-wall treatments
For 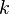 the boundary conditions imposed at the solid boundary are:
the boundary conditions imposed at the solid boundary are:
where 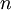 is the normal to the boundary.
is the normal to the boundary.
Moreover the centroid values in cells adjacent to solid wall are specified as
In the alternative approach 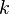 production terms is modified.
production terms is modified.
Automatic wall treatments
The purpose of automatic wall treatments is to make results insensitive with respect to wall mesh refinement. Many blending approaches have been proposed. The one by Menter takes advantage of the fact that the solution to 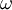 equations is known for both viscous and log layer
equations is known for both viscous and log layer
where 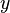 is the cell centroid distance from the wall. Using this a blending can take the following form:
is the cell centroid distance from the wall. Using this a blending can take the following form:
Note that for low 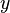 values the
values the 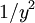 will dominate and therefore viscous value of
will dominate and therefore viscous value of 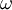 will be reproduced. Conversely, for larger values of
will be reproduced. Conversely, for larger values of 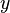 ,
, 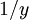 will be dominant and logarithmic value will be recovered.
will be dominant and logarithmic value will be recovered.
Subsequently Menter proposes also blending for friction velocity. Friction velocity for viscous and logarithmic region are:
And the blending suggested:
FLUENT
Both k- omega models (std and sst) are available as low-Reynolds-number models as well as high-Reynolds-number models.
The wall boundary conditions for the k equation in the k- omega models are treated in the same way as the k equation is treated when enhanced wall treatments are used with the k- epsilon models.
This means that all boundary conditions for
- wall-function meshes will correspond to the wall function approach, while for the
- fine meshes, the appropriate low-Reynolds-number boundary conditions will be applied.
In Fluent, that means:
If the Transitional Flows option is enabled in the Viscous Model panel, low-Reynolds-number variants will be used, and, in that case, mesh guidelines should be the same as for the enhanced wall treatment
(y+ at the wall-adjacent cell should be on the order of y+ = 1. However, a higher y+ is acceptable as long as it is well inside the viscous sublayer (y+ < 4 to 5).)
If Transitional Flows option is not active, then the mesh guidelines should be the same as for the wall functions.
(For [...] wall functions, each wall-adjacent cell's centroid should be located within the log-law layer, 30 < y+ < 300. A y+ value close to the lower bound y+ = 30 is most desirable.)
References
- Menter, F., Esch, T. (2001), "Elements of industrial heat transfer predictions", 'COBEM 2001, 16th Brazilian Congress of Mechanical Engineering.'.
- ANSYS (2006), "FLUENT Documentation", .

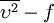 model
model
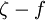 model
model


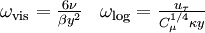
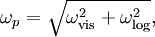

![u_\tau = \sqrt[4]{(u_\tau^{\text{vis}})^4 + (u_\tau^{\text{log}})^4},](/W/images/math/8/6/d/86dc5093c131963cbd5a3a4e0e74dfd1.png)