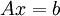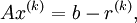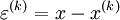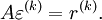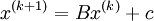Iterative methods

From CFD-Wiki

We seek the solution to the linear system of equations

Iterative methods, unlike direct methods, generate a sequence of approximate solutions to the system that (hopefully) converges to the exact solution. After k iterations, we obtain an approximation to the exact solution as:

where 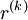is the residual after k iterations.
Defining

as the difference between the exact and approaximate solution, we obtain

The purpose of iterations is to drive this residual to zero.

Stationary Iterative Methods

Iterative methods that can be expressed in the simple form

when neither B nor c depend upon the iteration count (k), the iterative method is called stationary iterative method. Some of the stationary iterative methods are

1. Jacobi method
2. Gauss-Seidel method
3. Successive Overrelaxation (SOR) method and
4. Symmetric Successive Overrelaxation (SSOR) method

The convergence of such iterative methods can be investigated using the Fixed point theorem.

Nonstationary Iterative Methods

When during the iterations B and c changes during the iterations, the method is called Nonstationary Iterative Method. Typically, constants B and c are computed by taking inner products of residuals or other vectors arising from the iterative method.

Some examples are:

1. Conjugate Gradient Method (CG)
2. MINRES and SYMMLQ
3. Generalized Minimal Residual (GMRES)
4. BiConjugate Gradient (BiCG)
5. Quasi-Minimal Residual (QMR)
6. Conjugate Gradient Squared Method (CGS)
7. BiConjugate Gradient Stabilized (Bi-CGSTAB)
8. Chebyshev Iteration