Mesh classification
From CFD-Wiki
<< Introduction | Mesh Classification | Structured Mesh Generation>>
As CFD has developed, better algorithms and more computational power has become available to CFD analysts, resulting in diverse solver techniques. One of the direct results of this development has been the expansion of available mesh elements and mesh connectivity (how cells are connected to one another). The easiest classifications of meshes are based upon the connectivity of a mesh or on the type of elements present.
Contents |
Connectivity-Based Classification
The most basic form of mesh classification is based upon the connectivity of the mesh: structured or unstructured.
Structured Meshes
A structured mesh is characterized by regular connectivity that can be expressed as a two or three dimensional array. This restricts the element choices to quadrilaterals in 2D or hexahedra in 3D. The above example mesh is a structured mesh, as we could store the mesh connectivity in a 40 by 12 array. The regularity of the connectivity allows us to conserve space since neighborhood relationships are defined by the storage arrangement. Additional classification can be made upon whether the mesh is conformal or not.
Unstructured Meshes
An unstructured mesh is characterized by irregular connectivity is not readily expressed as a two or three dimensional array in computer memory. This allows for any possible element that a solver might be able to use. Compared to structured meshes, the storage requirements for an unstructured mesh can be substantially larger since the neighborhood connectivity must be explicitly stored.
Hybrid Meshes
A hybrid mesh is a mesh that contains structured portions and unstructured portions. Note that this definition requires knowledge of how the mesh is stored (and used). There is disagreement as to the correct application of the terms "hybrid" and "mixed." The term "mixed" is usually applied to meshes that contain elements associated with structured meshes and elements associated with unstructured meshes (presumably stored in an unstructured fashion).
Element-Based Classification
Meshes can also be classified based upon the dimension and type of elements present. Depending upon the analysis type and solver requirements, meshes generated could be 2-dimensional (2D) or 3-dimensional (3D). Common elements in 2D are triangles or rectangles, and common elements in 3D are tetrahedra or bricks. As noted above, some connectivity choices limit the types of element present, so there is some overlap between connectivity-based and element-based classification.
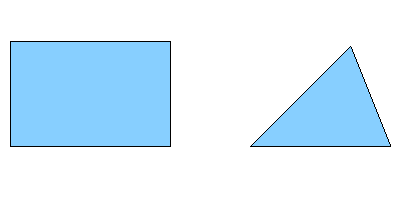
For a 2D mesh, all mesh nodes lie in a given plane. In most cases, 2D mesh nodes lie in the XY plane, but can also be confined to another Cartesian or user defined plane. Most popular 2D mesh elements are quadrilaterals (also known as quads) and triangles (tris), shown below.
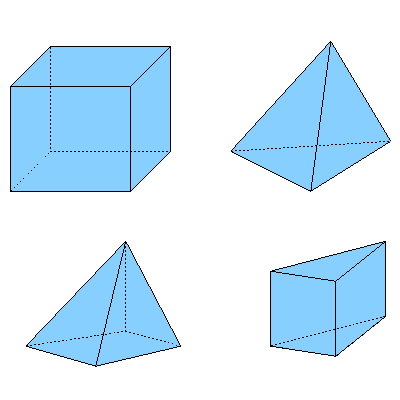
3D mesh nodes are not constrained to lie in a single plane. Most popular 3D mesh elements are hexahedra (also known as hexes or hex elements), tetrahedra (tets), square pyramids (pyramids) and extruded triangles (wedges or triangular prisms), shown below. It is worth noting that all these elements are bounded by faces belonging to the above mentioned 2D elements. Some of the current solvers also support polyhedral elements, which can be bounded by any number and types of faces.
Since all 3D elements are bounded by 2D elements, it is obvious that 3D meshes have exposed 2D elements at boundaries. Most of the meshing packages and solvers prefer to club exposed elements together in what is known as a surface mesh (for the purposes of applying boundary conditions, rendering meshed domains and visualizing results). A surface mesh does not have to be 2D, since volume meshes may conform to domains with non-planar boundaries. Many meshing algorithms start by meshing bounding surfaces of a domain before filling the interior with mesh nodes (such algorithms are also known as boundary to interior algorithms). For such algorithms, generation of good quality surface meshes is of prime importance, and much research has been done in the field of efficient and good quality surface mesh generation. Since surface meshes are geometrically somewhere between 2D and 3D meshes, they are also sometimes known as 2.5D meshes.
<< Introduction | Mesh Classification | Structured Mesh Generation>>