Finite element
From CFD-Wiki
The finite element method belongs to the class of weighted residual methods. It is a very powerful method, yet its basic principle is simple and interesting. The differential equation governing the transport of a scalar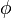 
is first written as
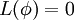
We then assume an approximate solution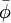 
of the form
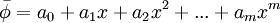
where the a's are unknown coefficients that are to be determined. For an initial value, it is clear that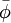 
does not satisfy the governing PDE, therfore leaving a residual R defined as
The idea is to drive the residual to zero by performing the convolution of R with a certain weight function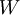 
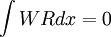
By choosing a succession of weight functions, one can generate as many equations as there are unknowns (the a's) thus yielding a albegraic system of equations.
The method can be viewed as a minimization problem. In fact, most discretization methods have this concept built in which is a fundamental principle in the theory of iterative methods.
