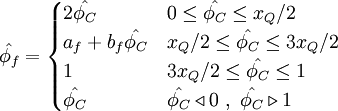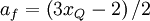Fromm based Schemes - structured grids

From CFD-Wiki

Revision as of 20:18, 14 October 2005 by Michail (Talk | contribs)

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)

$\hat{\phi_{f}}= \begin{cases} 2 \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq \frac{1}{4} \\ \frac{1}{4} + \hat{\phi_{C}} & \frac{1}{4} \leq \hat{\phi_{C}} \leq \frac{3}{4} \\ 1 & \frac{3}{4} \leq \hat{\phi_{C}} \leq 1 \\ \widehat{\phi_{C}} & \widehat{\phi_{C}} \triangleleft 0 \ , \ \widehat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

Normalized variables - non-uniform grids

$\hat{\phi_{f}}= \begin{cases} 2 \hat{\phi_{C}} & 0 \leq \hat{\phi_{C}} \leq x_{Q}/2 \\ a_{f} + b_{f} \hat{\phi_{C}} & x_{Q}/2 \leq \hat{\phi_{C}} \leq 3 x_{Q}/2 \\ 1 & 3 x_{Q}/2 \leq \hat{\phi_{C}} \leq 1 \\ \hat{\phi_{C}} & \hat{\phi_{C}} \triangleleft 0 \ , \ \hat{\phi_{C}} \triangleright 1 \end{cases}$

(2)

where

$a_{f}= \left( 3 x_{Q} - 2 \right)/2$

(2)

$b_{f}= \left( 1 - x_{Q} \right) / x_{Q}$

(2)

van Leer limiter

van Albada

Bounded Fromm

G.D. Van Albada, B.Van Leer, W.W.Roberts

A comparative study of computational methods in cosmic gas dynamics

Astron. Astrophysics, Vol. 108, p.76, 1982

OSPRE

bounded Fromm

Waterson [1995]

N.P.Waterson, H.Deconinck.

A unified approach to the design and application of bounded high-order convection schemes

In C. Taylor and P.Durbetaki, editors, Proc. Ninth Int. Conf. on Numer. Method. Laminar and turbulent Flow, pages 203-214, Pineride Press, Swansea, 1995

Fromm based Schemes - structured grids

From CFD-Wiki

Contents

Fromm scheme

MUSCL - Monotonic Upwind Scheme for Conservation Laws

van Leer limiter

van Albada

OSPRE

Views

My wiki

wiki navigation

wiki search

wiki toolbox