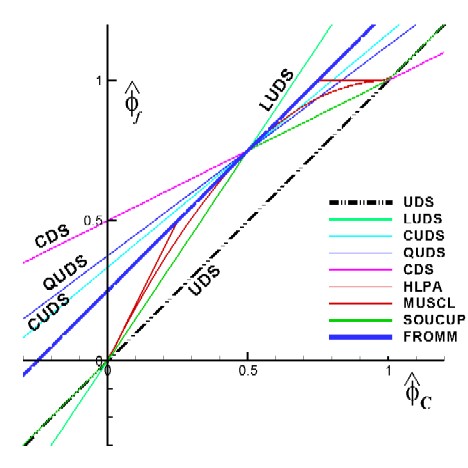
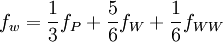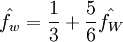Linear Schemes - structured grids
From CFD-Wiki
Linear
SOU - Second Order Upwind (also LUDS or UDS-2)
S.P.Vanka ({{{year}}}), "Second-order upwind differencing ina recirculating flow", AIAA J., 25, 1435-1441.
R.F.Warming and R.M. Beam (1976), "Upwind second order difference schemes and applications in aerodynamics flows", AIAA J. 14 (1976) 1241-1249.
Skew - Upwind
G.D.Raithby , Skew upstream differencing schemes for problems involving fluid flow, Computational Methods Applied Mech. Engineering, 9, 153-164 (1976)
QUICK - Quadratic Upwind Interpolation for Convective Kinematics (also UDS-3 or QUDS)
B.P.Leonard, A stable and accurate modelling procedure based on quadratic interpolation, Comput. Methods Appl. Mech. Engrg. 19 (1979) 58-98
Usual variables
|
| (2) |
|
| (2) |
|
| (2) |
Normalised variables (uniform grid)
|
| (2) |
Normalised variables (non-uniform grid)
|
| (2) |
|
| (2) |
|
| (2) |
LUS - Linear Upwind Scheme
H.C.Price, R.S. Varga and J.E.Warren , Application of oscillation matrices to diffusion-convection equations, Journal Math. and Phys., Vol. 45, p.301, (1966)
Fromm - Fromm's Upwind Scheme
CUDS - Cubic Upwind Difference Scheme (also CUS or UDS-4)
In CUDS (UDS-4) for interpolation of function is used three upwind nodes and one node downstream.
usual variables
|
| (2) |
normalised variables (uniform grids)
|
| (2) |
R.K. Aragval
A third-order-accurate upwind scheme for Navier-Stokes solution at high Reynolds numbers
Paper No. AIAA-81-0112, AIAA 19th Aerospace Science Meeting, St. Louis, 1982.
CUI - Cubic Upwind Interpolation
B.P. Leonard
A survey of finite differences of opinion on numerical muddling of incompressible defective confusion equation
paper in ASME, Applied Mechanics Division, Winter Annual Meeting, 1979

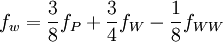


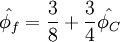
![\begin{matrix}
\hat{f_{w}} & = \left\{ \left( 1 + C_{1} \right) \left( 1 - C_{2} \right)\hat{f_{W}} + C_{2} \left[ 1 - \frac{C_{1} \left( 1 - C_{2} \right) }{ C_{1} + C_{2} } \right] \right\} U^{+}_{w} + \\
+ & \left\{ C_{2} \left( 1 + C_{3} \right) \hat{f_{P}} + \left( 1 - C_{2} \right) \left[ 1 - \frac{C_{2} C_{3} }{ 1- C_{2} + C_{3} } \right] \right\} U^{-}_{w}
\end{matrix}](/W/images/math/6/8/b/68bac8a6883cdc4dcc86875cdfff006b.png)
![\begin{matrix}
\hat{\phi_{w}} & = \left\{ \left( 1 + C_{1} \right) \left( 1 - C_{2} \right)\hat{\phi_{W}} + C_{2} \left[ 1 - \frac{C_{1} \left( 1 - C_{2} \right) }{ C_{1} + C_{2} } \right] \right\} U^{+}_{w} + \\
+ & \left\{ C_{2} \left( 1 + C_{3} \right) \hat{\phi_{P}} + \left( 1 - C_{2} \right) \left[ 1 - \frac{C_{2} C_{3} }{ 1- C_{2} + C_{3} } \right] \right\} U^{-}_{w}
\end{matrix}](/W/images/math/9/2/5/925db1d1d212b7ae8fecb9ac1cf4a7ef.png)
![\begin{matrix}
\hat{\phi_{f}} & = \left\{ \left( 1 + C_{1} \right) \left( 1 - C_{2} \right)\hat{\phi_{C}} + C_{2} \left[ 1 - \frac{C_{1} \left( 1 - C_{2} \right) }{ C_{1} + C_{2} } \right] \right\} U^{+}_{f} + \\
+ & \left\{ C_{2} \left( 1 + C_{3} \right) \hat{\phi_{D}} + \left( 1 - C_{2} \right) \left[ 1 - \frac{C_{2} C_{3} }{ 1- C_{2} + C_{3} } \right] \right\} U^{-}_{f}
\end{matrix}](/W/images/math/0/b/8/0b89df8d7877d9716eaa0ea033f8d368.png)