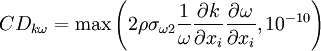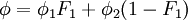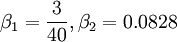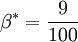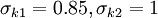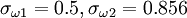SST k-omega model
From CFD-Wiki
Revision as of 08:19, 11 October 2005 by Jonas Bredberg (Talk | contribs)
Contents |
Kinematic Eddy Viscosity
Turbulence Kinetic Energy
Specific Dissipation Rate
Closure Coefficients and Auxilary Relations
References
- Menter, F.R. (1994), "Two-equation eddy-viscosity turbulence models for engineering applications", AIAA Journal, vol. 32, pp. 269-289.

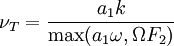
![{{\partial k} \over {\partial t}} + U_j {{\partial k} \over {\partial x_j }} = P_k - \beta ^* k\omega + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma_{k1} \nu _T } \right){{\partial k} \over {\partial x_j }}} \right]](/W/images/math/2/6/0/260b982db012f9ae1575154ade40b566.png)
![{{\partial \omega } \over {\partial t}} + U_j {{\partial \omega } \over {\partial x_j }} = \alpha S^2 - \beta \omega ^2 + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma_{\omega 1} \nu _T } \right){{\partial \omega } \over {\partial x_j }}} \right] + 2( 1 - F_1 ) \sigma_{\omega 2} {1 \over \omega} {{\partial k } \over {\partial x_i}} {{\partial \omega } \over {\partial x_i}}](/W/images/math/1/d/7/1d76c55d743546e29debcc8945e5d4e6.png)
![F_2=\mbox{tanh} \left[ \left[ \mbox{max} \left( { 2 \sqrt{k} \over \beta^* \omega y } , { 500 \nu \over y^2 \omega } \right) \right]^2 \right]](/W/images/math/8/7/d/87d29560b46100813cef49e9f861f1cc.png)
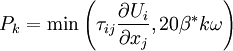
![F_1=\mbox{tanh} \left\{ \left\{ \mbox{min} \left[ \mbox{max} \left( {\sqrt{k} \over \beta ^* \omega y}, {500 \nu \over y^2 \omega} \right) , {4 \sigma_{\omega 2} k \over CD_{k\omega} y^2} \right] \right\} ^4 \right\}](/W/images/math/1/4/3/1438132576e08de1da7394c694172485.png)