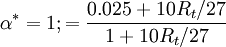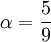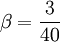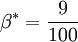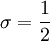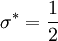Wilcox's k-omega model
From CFD-Wiki
Revision as of 10:06, 6 October 2005 by Jonas Bredberg (Talk | contribs)
Contents |
Kinematic Eddy Viscosity
Turbulence Kinetic Energy
Specific Dissipation Rate
Closure Coefficients and Auxilary Relations
References
- Wilcox, D.C. (1988), "Re-assessment of the scale-determining equation for advanced turbulence models", AIAA Journal, vol. 31, pp. 1414-1421.

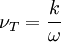
![{{\partial k} \over {\partial t}} + U_j {{\partial k} \over {\partial x_j }} = \tau _{ij} {{\partial U_i } \over {\partial x_j }} - \beta ^* k\omega + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma ^* \nu _T } \right){{\partial k} \over {\partial x_j }}} \right]](/W/images/math/1/a/4/1a436edcf81f2ccbdf53dfa7dd9e0550.png)
![{{\partial \omega } \over {\partial t}} + U_j {{\partial \omega } \over {\partial x_j }} = \alpha {\omega \over k}\tau _{ij} {{\partial U_i } \over {\partial x_j }} - \beta \omega ^2 + {\partial \over {\partial x_j }}\left[ {\left( {\nu + \sigma \nu _T } \right){{\partial \omega } \over {\partial x_j }}} \right]](/W/images/math/b/3/6/b361dbe1c46fcbcbf1795a2997a00e09.png)