Incomplete Cholesky Factorization

From CFD-Wiki

Cholesky Factorization

When the square matrix A is symmetric and positive definite then it has an efficient triangular decomposition. Symmetric means that a_ij = a_ji for i,j = 1, ... , N. While positive definite means that

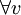
In cholesky factorization we construct a lower triangular matrix L whose transpose L^T can itself serve as upper triangular part.
In other words we have
L L^T = A

Algorithm for full matrix A

We have by definition
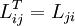
From this we can easily obtain

for := 1 step 1 until N do

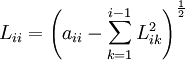
and
 ; where j = i+1, i+2, ..., N

end (i-loop)