Introduction to turbulence/Stationarity and homogeneity
From CFD-Wiki
Processes statistically stationary in time
Many random processes have the characteristic that their statistical properties do not appear to depend directly on time, even though the random variables themselves are time-dependent. For example, consider the signals shown in Figures 2.2 and 2.5
When the statistical properties of a random process are independent of time, the random process is said to be stationary. For such a process all the moments are time-independent, e.g., 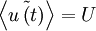 , etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent.
, etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent.
An alternative way of looking at stationarity is to note that the statistics of the process are independent of the origin in time. It is obvious from the above, for example, that if the statistics of a process are time independent, then 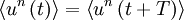 , etc., where
, etc., where 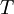 is some arbitrary translation of the origin in time. Less obvious, but equally true, is that the product
is some arbitrary translation of the origin in time. Less obvious, but equally true, is that the product 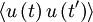 depends only on time difference
depends only on time difference 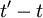 and not on
and not on 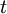 (or
(or 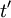 ) directly. This consequence of stationarity can be extended to any product moment. For example
) directly. This consequence of stationarity can be extended to any product moment. For example 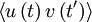 can depend only on the time difference
can depend only on the time difference 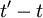 . And
. And 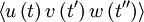 can depend only on the two time differences
can depend only on the two time differences 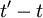 and
and 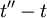 (or
(or 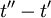 ) and not
) and not 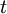 ,
, 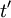 or
or  directly.
directly.
The autocorrelation
One of the most useful statistical moments in the study of stationary random processes (and turbulence, in particular) is the autocorrelation defined as the average of the product of the random variable evaluated at two times, i.e. 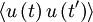 . Since the process is assumed stationary, this product can depend only on the time difference
. Since the process is assumed stationary, this product can depend only on the time difference 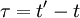 . Therefore the autocorrelation can be written as:
. Therefore the autocorrelation can be written as:
|
| (1) |

