Velocity-pressure coupling
From CFD-Wiki
If we consider the discretised form of the Navier-Stokes system, the form of the equations shows linear dependence of velocity on pressure and vice-versa. This inter-equation coupling is called velocity pressure coupling. A special treatment is required in order to velocity-pressure coupling. The methods such as:
- SIMPLE
- SIMPLER
- SIMPLEC
- PISO
provide an useful means of doing this for segregated solvers. However it is possible to solve the system of Navier-Stokes equations in coupled manner, taking care of inter equation coupling in a single matrix.
Contents |
Formulation
we have at each cell descretised equation in this form,
 ;
;
we have
For continuity :
so we get:
this gives us:
defining 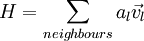
from this a pressure correction equation could be formed as:
This is a poisson equation.
Here the gradients could be used from previous iteration.
SIMPLE
See SIMPLE algorithm
SIMPLER
SIMPLEC
PISO
See PISO algorithm
Return to:


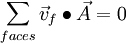
![\left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face} - \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face} = 0](/W/images/math/f/7/e/f7e0da565cdb617ce4f3124203e503c1.png)
![\left[ {\frac{{\sum\limits_{neighbours} {a_l } \vec v_l }}{{a_p }}} \right]_{face} = \left[ {\frac{{\nabla p}}{{a_p V}}} \right]_{face}](/W/images/math/d/9/a/d9a701a1aaad2b208b62474614781147.png)
![\left[ {\frac{1}{{a_p }}H} \right]_{face} = \left[ {\frac{1}{{a_p }}\frac{{\nabla p}}{V}} \right]_{face}](/W/images/math/b/e/1/be109456135e08608800a492d37b823a.png)
![\left[ {\frac{1}{{a_p }}H} \right]_{face} - \left[ {\frac{1}{{a_p }}\frac{{\nabla p^* }}{V}} \right]_{face} = \left[ {\frac{1}{{a_p }}\frac{{\nabla p^' }}{V}} \right]_{face}](/W/images/math/0/4/3/043590859f53e135dd2724fe98e03b71.png)