Incomplete Cholesky Factorization
From CFD-Wiki
Cholesky Factorization
When the square matrix A is symmetric and positive definite then it has an efficient triangular decomposition. Symmetric means that aij = aji for i,j = 1, ... , N. While positive definite means that

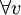
In cholesky factorization we construct a lower triangular matrix L whose transpose LT can itself serve as upper triangular part.
In other words we have
L  LT = A
LT = A
