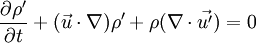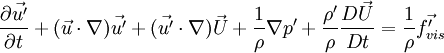Hydrodynamic/acoustic splitting
From CFD-Wiki
(Difference between revisions)
| Line 2: | Line 2: | ||
perturbed compressible ones as, | perturbed compressible ones as, | ||
| - | <math>\rho(\vec{x},t)=\rho_0+\rho'(\vec{x},t) | + | <math>\rho(\vec{x},t)=\rho_0+\rho'(\vec{x},t) </math> |
| + | |||
<math>\vec{u}(\vec{x},t)=\vec{U}(\vec{x},t)+\vec{u'}(\vec{x},t)</math> | <math>\vec{u}(\vec{x},t)=\vec{U}(\vec{x},t)+\vec{u'}(\vec{x},t)</math> | ||
| + | |||
<math>p(\vec{x},t)=P(\vec{x},t)+p'(\vec{x},t)</math> | <math>p(\vec{x},t)=P(\vec{x},t)+p'(\vec{x},t)</math> | ||
| Line 12: | Line 14: | ||
<math>\frac{\partial\rho'}{\partial t}+(\vec{u}\cdot\nabla)\rho'+\rho(\nabla\cdot\vec{u'})=0</math> | <math>\frac{\partial\rho'}{\partial t}+(\vec{u}\cdot\nabla)\rho'+\rho(\nabla\cdot\vec{u'})=0</math> | ||
| + | |||
<math>\frac{\partial\vec{u'}}{\partial | <math>\frac{\partial\vec{u'}}{\partial | ||
t}+(\vec{u}\cdot\nabla)\vec{u'}+(\vec{u'}\cdot\nabla)\vec{U}+\frac{1}{\rho}\nabla | t}+(\vec{u}\cdot\nabla)\vec{u'}+(\vec{u'}\cdot\nabla)\vec{U}+\frac{1}{\rho}\nabla | ||
p'+\frac{\rho'}{\rho}\frac{D\vec{U}}{Dt}=\frac{1}{\rho}\vec{f'_{vis}}</math> | p'+\frac{\rho'}{\rho}\frac{D\vec{U}}{Dt}=\frac{1}{\rho}\vec{f'_{vis}}</math> | ||
| + | |||
<math>\frac{{\partial p'}}{{\partial t}}\!+\!(\vec u \cdot \nabla )p'\!+\!\gamma p(\nabla \cdot \vec u') + (\vec | <math>\frac{{\partial p'}}{{\partial t}}\!+\!(\vec u \cdot \nabla )p'\!+\!\gamma p(\nabla \cdot \vec u') + (\vec | ||
u' \cdot \nabla )P = - \frac{{DP}}{{Dt}} + (\gamma - 1)\left( {\Phi - \nabla \cdot \vec q} \right)</math> | u' \cdot \nabla )P = - \frac{{DP}}{{Dt}} + (\gamma - 1)\left( {\Phi - \nabla \cdot \vec q} \right)</math> | ||
Revision as of 21:30, 30 July 2008
In the hydrodynamic/acoustic splitting method, the total flow variables are decomposed into the incompressible variables and the perturbed compressible ones as,
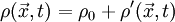
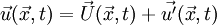

The incompressible variables represent the hydrodynamic flow field, while the acoustic fluctuations and other compressibility effects are resolved by the perturbed quantities denoted by ('). The original full perturbed compressible equations (PCE) to calculate the perturbed quantities can be derived by subtracting the incompressible Navier-Stokes equations from the compressible ones. The PCE recently revised by Seo and Moon are written in a vector form as,