Introduction to turbulence/Stationarity and homogeneity
From CFD-Wiki
(Difference between revisions)
(→Processes statistically stationary in time) |
(→Processes statistically stationary in time) |
||
| Line 2: | Line 2: | ||
Many random processes have the characteristic that their statistical properties do not appear to depend directly on time, even though the random variables themselves are time-dependent. For example, consider the signals shown in Figures 2.2 and 2.5 | Many random processes have the characteristic that their statistical properties do not appear to depend directly on time, even though the random variables themselves are time-dependent. For example, consider the signals shown in Figures 2.2 and 2.5 | ||
| + | |||
| + | When the statistical properties of a random process are independent of time, the random process is said to be ''stationary''. For such a process all the moments are time-independent, e.g., <math> \left\langle \tilde{ u \left( t \right)} \right\rangle = U </math>, etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent. | ||
== The autocorrelation == | == The autocorrelation == | ||
Revision as of 20:09, 1 January 2008
Processes statistically stationary in time
Many random processes have the characteristic that their statistical properties do not appear to depend directly on time, even though the random variables themselves are time-dependent. For example, consider the signals shown in Figures 2.2 and 2.5
When the statistical properties of a random process are independent of time, the random process is said to be stationary. For such a process all the moments are time-independent, e.g.,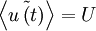 
, etc. In fact, the probability density itself is time-independent, as should be obvious from the fact that the moments are time independent.
