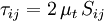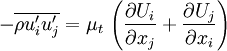Two equation turbulence models
From CFD-Wiki
m (small improvements) |
|||
| Line 1: | Line 1: | ||
Two-equation turbulence models are one of the most common type of turbulence models. Models like the [[K-epsilon models|k-epsilon model]] and the [[K-omega models|k-omega model]] have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed. | Two-equation turbulence models are one of the most common type of turbulence models. Models like the [[K-epsilon models|k-epsilon model]] and the [[K-omega models|k-omega model]] have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed. | ||
| - | By definition, two-equation models | + | By definition, two-equation models include two extra transport equations to represent the turbulent properties of the flow. Most often one of the transported variables is the [[Turbulent kinetic energy|turbulent kinetic energy]], <math>k</math>. The second transported variable varies depending on what type of two-equation model it is. Common choices are the turbulent [[Dissipation|dissipation]], <math>\epsilon</math>, or the [[Specific dissipation|specific dissipation]], <math>\omega</math>. The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, <math>k</math>, determines the energy in the turbulence. |
| - | The basis for all two-equation models is the [[Boussinesq eddy viscosity assumption]], which postulates that the [[Reynolds stress tensor]] is proportional to the mean strain rate tensor: | + | The basis for all two-equation models is the [[Boussinesq eddy viscosity assumption]], which postulates that the [[Reynolds stress tensor]], <math>\tau_{ij}</math>, is proportional to the mean strain rate tensor, <math>S_{ij}</math>, and can be written in the following way: |
:<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}</math> | :<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}</math> | ||
| - | + | Where <math>\mu_t</math> is a scalar property called the [[Eddy viscosity|eddy viscosity]]. The same equation can be written more explicitly as: | |
:<math> -\overline{\rho u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right)</math> | :<math> -\overline{\rho u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right)</math> | ||
{{stub}} | {{stub}} | ||
Revision as of 20:50, 9 May 2006
Two-equation turbulence models are one of the most common type of turbulence models. Models like the k-epsilon model and the k-omega model have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed.
By definition, two-equation models include two extra transport equations to represent the turbulent properties of the flow. Most often one of the transported variables is the turbulent kinetic energy,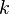 
. The second transported variable varies depending on what type of two-equation model it is. Common choices are the turbulent dissipation, 
, or the specific dissipation,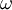 
. The second variable can be thought of as the variable that determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, 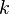, determines the energy in the turbulence.
The basis for all two-equation models is the Boussinesq eddy viscosity assumption, which postulates that the Reynolds stress tensor,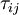 
, is proportional to the mean strain rate tensor, 
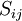, and can be written in the following way:
Where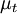 
is a scalar property called the eddy viscosity. The same equation can be written more explicitly as:
