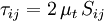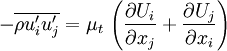Two equation turbulence models
From CFD-Wiki
m (Two equation models moved to Two equation turbulence models) |
(more content, not by far finished yet, will write more) |
||
| Line 1: | Line 1: | ||
| - | Two-equation models | + | Two-equation turbulence models are one of the most common type of turbulence models. Models like the <math>k-\epsilon</math> model and the <math>k-\omega</math> model have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed. |
| - | + | By definition, two-equation models have two extra transport equations to represent the turbulent properties of the flow. Most often one of the transported variables is the [[Turbulent energy|turbulent energy]], <math>k</math>. The second transported variable can vary depending on what type of two-equation model it is. Common choices are the turbulent [[Dissipation|dissipation]], <math>\epsilon</math> or the [[Specific dissipation|specific dissipation]], <math>\omega</math>. In any case the second variable should be thought of as the variable that transports and determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, <math>k</math>, determines the strength or energy in the turbulence. | |
| + | |||
| + | The basis for all two-equation models is the [[Boussinesq eddy viscosity assumption]], which postulates that the [[Reynolds stress tensor]] is proportional to the strain rate tensor: | ||
| + | |||
| + | :<math>\tau_{ij} = 2 \, \mu_t \, S_{ij}</math> | ||
| + | |||
| + | Or the same equation written out more explicitly: | ||
| + | |||
| + | :<math> -\overline{\rho u'_i u'_j} = \mu_t \, \left( \frac{\partial U_i}{\partial x_j} + \frac{\partial U_j}{\partial x_i} \right)</math> | ||
{{stub}} | {{stub}} | ||
Revision as of 22:59, 8 May 2006
Two-equation turbulence models are one of the most common type of turbulence models. Models like the 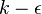 model and the
model and the 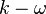 model have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed.
model have become industry standard models and are commonly used for most type of engineering problems. Two-equation turbulence models are also very much still an active area of research and new refined two-equation models are still being developed.
By definition, two-equation models have two extra transport equations to represent the turbulent properties of the flow. Most often one of the transported variables is the turbulent energy, 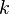 . The second transported variable can vary depending on what type of two-equation model it is. Common choices are the turbulent dissipation,
. The second transported variable can vary depending on what type of two-equation model it is. Common choices are the turbulent dissipation,  or the specific dissipation,
or the specific dissipation, 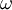 . In any case the second variable should be thought of as the variable that transports and determines the scale of the turbulence (length-scale or time-scale), whereas the first variable,
. In any case the second variable should be thought of as the variable that transports and determines the scale of the turbulence (length-scale or time-scale), whereas the first variable, 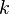 , determines the strength or energy in the turbulence.
, determines the strength or energy in the turbulence.
The basis for all two-equation models is the Boussinesq eddy viscosity assumption, which postulates that the Reynolds stress tensor is proportional to the strain rate tensor:
Or the same equation written out more explicitly: