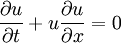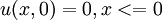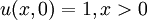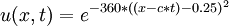Non linear wave propagation
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
== Problem definition == | == Problem definition == | ||
| - | :<math> \frac{\partial u}{\partial t}+ | + | :<math> \frac{\partial u}{\partial t}+ u \frac{\partial u}{\partial x}=0 |
</math> | </math> | ||
== Domain == | == Domain == | ||
| - | x=[ | + | x=[-5,10] |
== Initial Condition == | == Initial Condition == | ||
| - | :<math> u(x,0)= | + | :<math> u(x,0)=0 ,x <=0 </math> |
| - | + | :<math> u(x,0)=1 ,x >0 </math> | |
== Boundary condition == | == Boundary condition == | ||
u[0]=0,u[imax]=u[imax-1](x[imax]=1.0) | u[0]=0,u[imax]=u[imax-1](x[imax]=1.0) | ||
| Line 15: | Line 15: | ||
c=1,t=0.25 | c=1,t=0.25 | ||
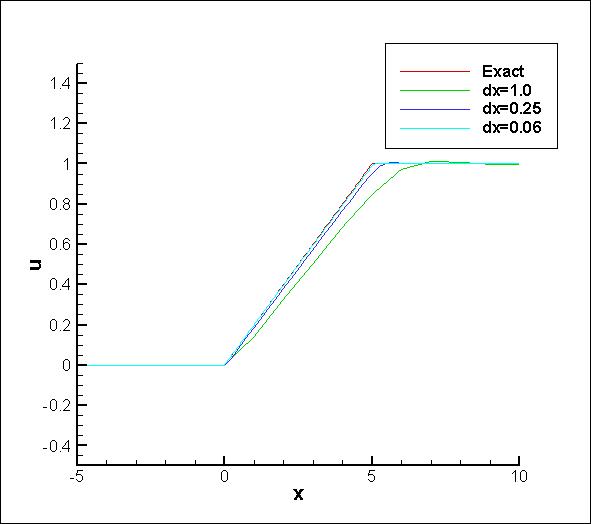
== Results == | == Results == | ||
| - | [[Image: | + | [[Image:Nonlinear_1d.jpg]] |
== Reference == | == Reference == | ||
Revision as of 01:48, 25 December 2005
Contents |
Problem definition
Domain
x=[-5,10]
Initial Condition
Boundary condition
u[0]=0,u[imax]=u[imax-1](x[imax]=1.0)
Exact solution
Numerical method
c=1,t=0.25