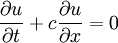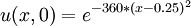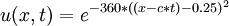Non linear wave propagation
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
== Problem definition == | == Problem definition == | ||
| - | + | :<math> \frac{\partial u}{\partial t}+ c \frac{\partial u}{\partial x}=0 | |
| - | == Domain | + | </math> |
| - | + | == Domain == | |
| + | x=[0,1] | ||
== Initial Condition == | == Initial Condition == | ||
| + | :<math> u(x,0)=e^{-360*{(x-0.25)}^2}</math> | ||
== Boundary condition == | == Boundary condition == | ||
| + | u[0]=0,u[imax]=u[imax-1](x[imax]=1.0) | ||
| + | == Exact solution == | ||
| + | :<math> u(x,t)=e^{-360*{((x-c*t)-0.25)}^2}</math> | ||
== Numerical method == | == Numerical method == | ||
| + | c=1,t=0.25 | ||
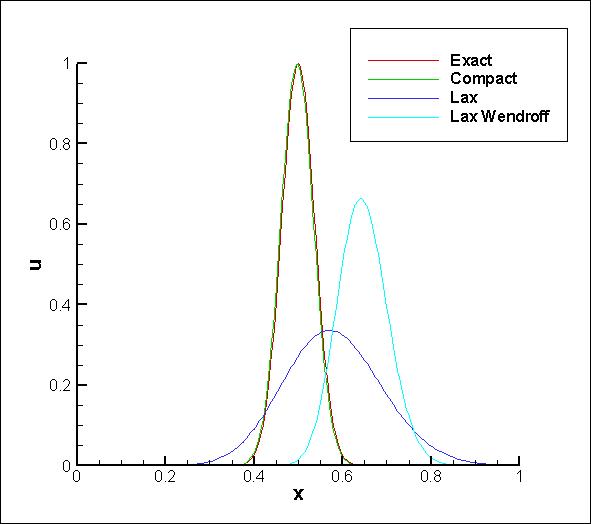
| + | == Results == | ||
| + | [[Image:Linear_1d.jpg]] | ||
| - | == | + | == Reference == |
Revision as of 01:43, 25 December 2005
Contents |
Problem definition
Domain
x=[0,1]
Initial Condition
Boundary condition
u[0]=0,u[imax]=u[imax-1](x[imax]=1.0)
Exact solution
Numerical method
c=1,t=0.25