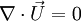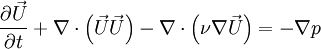Solution of Navier-Stokes equations
From CFD-Wiki
(Difference between revisions)
(fixed dot product notation) |
|||
| Line 1: | Line 1: | ||
For the incompressible flows, the Navier-Stokes equation could be written in the form: <br> | For the incompressible flows, the Navier-Stokes equation could be written in the form: <br> | ||
:<math> | :<math> | ||
| - | \nabla \ | + | \nabla \cdot \vec U = 0 </math> <br> |
| - | :<math> {{\partial \vec U} \over {\partial t}} + \nabla \ | + | :<math> {{\partial \vec U} \over {\partial t}} + \nabla \cdot \left( {\vec U\vec U} \right) - \nabla \cdot\left( {\nu \nabla \vec U} \right) = - \nabla p </math> |
There are two important issues regarding Navier-Stokes equations: <br> | There are two important issues regarding Navier-Stokes equations: <br> | ||
Revision as of 20:29, 15 December 2005
For the incompressible flows, the Navier-Stokes equation could be written in the form:
There are two important issues regarding Navier-Stokes equations:
- Non linearity of momentum equations
- Pressure-velocity coupling
Segregated Solver
The solution scheme
- Solve Momentum equations (u,v,w)
- Solve pressure correction equation
- Correct fluxes and velocities
- Solve transport equations for other scalars
Coupled Solver
Return to Numerical Methods