Generic scalar transport equation
From CFD-Wiki
| Line 1: | Line 1: | ||
| - | A differential equation epxresses a certain conservation principle. Whether be it in electromagnetics, fluid dynamics, heat transfer, radiation, electronics... conservation principles are the basis for the derivation of differential or integro-differential equations. In this respect, any differential equation addresses a certain quantity as it dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quanitity. For example, the temperature of a fluid in a heated pipe is affected by convection due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a state state problem, with the absence of sources, a differential equation governing the temperature will definetely express a balance between convection and diffusion. | + | A differential equation epxresses a certain conservation principle. Whether be it in electromagnetics, fluid dynamics, heat transfer, radiation, electronics... conservation principles are the basis for the derivation of differential or integro-differential equations. In this respect, any differential equation addresses a certain quantity as it dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quanitity. For example, the temperature of a fluid in a heated pipe is affected by convection due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a state state problem, with the absence of sources, a differential equation governing the temperature will definetely express a balance between convection and diffusion. |
| - | A brief inspection of the equations governing various physical phenomena will reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation. | + | |
| - | For example, the conservation equation of a chemical species <math> c_i </math> is | + | A brief inspection of the equations governing various physical phenomena will reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation. For example, the conservation equation of a chemical species <math> c_i </math> is |
| - | <math> \frac{\partial{\rho c_i}}{\partial t} + \nabla \cdot (\rho \vec u c_i + \vec J) = R_i </math> | + | |
| - | where <math> \vec u </math> denotes the velocity field, <math> \vec J </math> denotes the diffusion flux the of the chemical species, and <math> R_i </math> denotes the rate of generation of <math> R_i </math> caused by the chemical reaction. | + | :<math> \frac{\partial{\rho c_i}}{\partial t} + \nabla \cdot (\rho \vec u c_i + \vec J) = R_i </math> |
| - | The '''x-momentum''' equation for a Newtonian fluid can be written as | + | |
| - | <math> \frac{\partial{\rho u}}{\partial t} + \nabla \cdot (\rho \vec u u ) =\nabla \cdot (\mu \nabla u ) - \frac {\partial p}{\partial x} + B_x + V_x </math> | + | where <math> \vec u </math> denotes the velocity field, <math> \vec J </math> denotes the diffusion flux the of the chemical species, and <math> R_i </math> denotes the rate of generation of <math> R_i </math> caused by the chemical reaction. |
| - | where <math> B_x </math> is the body force in the x-direction and <math>V_x</math> includes the viscous terms that are not expressed by <math>\nabla \cdot (\mu \nabla u )</math | + | |
| - | + | The '''x-momentum''' equation for a Newtonian fluid can be written as | |
| - | Upon inspection of the above equations, it can be infered that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by <math>\phi</math>, the '''generic''' differential equation is | + | |
| - | <math> \underbrace{ \frac{\partial{\rho \phi}}{\partial t}}_{Transient \ term} + \underbrace{ \nabla \cdot (\rho \vec u \phi )}_{Convection \ term} =\underbrace {\nabla \cdot (\Gamma \nabla \phi )}_{Diffusion \ term} + \underbrace {S_{\phi}}_{Source \ term}</math | + | :<math> \frac{\partial{\rho u}}{\partial t} + \nabla \cdot (\rho \vec u u ) =\nabla \cdot (\mu \nabla u ) - \frac {\partial p}{\partial x} + B_x + V_x </math> |
| - | + | ||
| - | where <math> \Gamma </math> is the '''diffusion''' coefficient or '''diffusivity''' | + | where <math> B_x </math> is the body force in the x-direction and <math>V_x</math> includes the viscous terms that are not expressed by <math>\nabla \cdot (\mu \nabla u )</math> |
| + | |||
| + | Upon inspection of the above equations, it can be infered that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by <math>\phi</math>, the '''generic''' differential equation is | ||
| + | |||
| + | :<math> \underbrace{ \frac{\partial{\rho \phi}}{\partial t}}_{Transient \ term} + \underbrace{ \nabla \cdot (\rho \vec u \phi )}_{Convection \ term} =\underbrace {\nabla \cdot (\Gamma \nabla \phi )}_{Diffusion \ term} + \underbrace {S_{\phi}}_{Source \ term}</math> | ||
| + | |||
| + | where <math> \Gamma </math> is the '''diffusion''' coefficient or '''diffusivity'''. | ||
Revision as of 06:20, 14 December 2005
A differential equation epxresses a certain conservation principle. Whether be it in electromagnetics, fluid dynamics, heat transfer, radiation, electronics... conservation principles are the basis for the derivation of differential or integro-differential equations. In this respect, any differential equation addresses a certain quantity as it dependent variable and thus expresses the balance between the phenomena affecting the evolution of this quanitity. For example, the temperature of a fluid in a heated pipe is affected by convection due to the solid-fluid interface, and due to the fluid-fluid interaction. Furthermore, temperature is also diffused inside the fluid. For a state state problem, with the absence of sources, a differential equation governing the temperature will definetely express a balance between convection and diffusion.
A brief inspection of the equations governing various physical phenomena will reveal that all of these equations can be put into a generic form thus allowing a systematic approach for a computer simulation. For example, the conservation equation of a chemical species  is
is
where 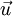 denotes the velocity field,
denotes the velocity field, 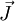 denotes the diffusion flux the of the chemical species, and
denotes the diffusion flux the of the chemical species, and 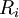 denotes the rate of generation of
denotes the rate of generation of 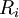 caused by the chemical reaction.
caused by the chemical reaction.
The x-momentum equation for a Newtonian fluid can be written as
where  is the body force in the x-direction and
is the body force in the x-direction and 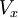 includes the viscous terms that are not expressed by
includes the viscous terms that are not expressed by 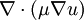
Upon inspection of the above equations, it can be infered that all the dependent variables seem to obey a generalized conservation principle. If the dependent variable (scalar or vector) is denoted by 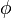 , the generic differential equation is
, the generic differential equation is
where 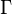 is the diffusion coefficient or diffusivity.
is the diffusion coefficient or diffusivity.