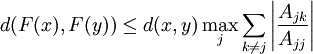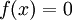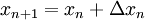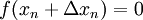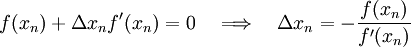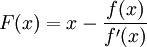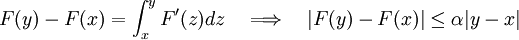Fixed point theorem
From CFD-Wiki
Revision as of 10:53, 19 October 2005
The fixed point theorem is a useful tool for proving existence of solutions and also for convergence of iterative schemes. In fact the latter is used to prove the former. If the problem is to find the solution of
then we convert it to a problem of finding a fixed point
Statement
Let 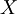 be a complete metric space with distance
be a complete metric space with distance
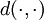 and let
and let 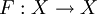 be contractive,
i.e., for some
be contractive,
i.e., for some 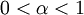 ,
,
Then there exists a unique fixed point 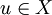 such that
such that
Proof
Choose any 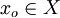 and define the sequence
and define the sequence 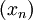 by
the following iterative scheme
by
the following iterative scheme
If we can show that the sequence 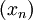 has a unique limit
independent of the starting value then we would have proved the existence of
the fixed point. The first step is to show that
has a unique limit
independent of the starting value then we would have proved the existence of
the fixed point. The first step is to show that 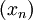 is a Cauchy
sequence.
is a Cauchy
sequence.

| 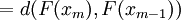
|
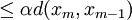
| |
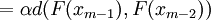
| |

| |

| |

| |
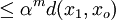
|
Now using the triangle inequality we get, for 
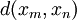
| 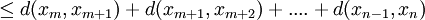
|
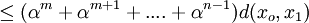
| |
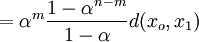
| |
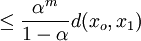
|
where the last inequality follows because 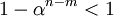 .
Now since
.
Now since  as
as 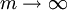 we see that
we see that
which proves that 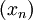 is a Cauchy sequence. Since
is a Cauchy sequence. Since 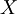 is complete, this sequence converges to a unique limit
is complete, this sequence converges to a unique limit 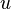 . It is
now left to show that the limit is a fixed point.
. It is
now left to show that the limit is a fixed point.
and since 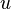 is the limit of the sequence we see that the right
hand side goes to zero so that
is the limit of the sequence we see that the right
hand side goes to zero so that
The uniqueness of the fixed point follows easily. Let 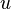 and
and
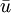 be two fixed points. Then
be two fixed points. Then
and since 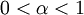 we conclude that
we conclude that
Application to solution of linear system of equations
We will apply the fixed point theorem to show the convergence of Jacobi iterations for the numerical solution of the linear algebraic system
under the condition that the matrix 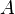 is diagonally dominant. Assuming
that the diagonal elements are non-zero, define the diagonal matrix
is diagonally dominant. Assuming
that the diagonal elements are non-zero, define the diagonal matrix
and rewriting we get
which is now in the form of a fixed point problem with
For measuring the distance between two vectors let us choose the maximum norm
We must show that 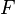 is a contraction mapping in this norm. Now
is a contraction mapping in this norm. Now
so that the j'th component is given by
From this we get
and
Hence the mapping is contractive if
which is just the condition of diagonal dominance of matrix 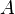 . Hence if
the matrix is diagonally dominant then the fixed point theorem assures us
that the Jacobi iterations will converge.
. Hence if
the matrix is diagonally dominant then the fixed point theorem assures us
that the Jacobi iterations will converge.
Application to Newton-Raphson method
Consider the problem of finding the roots of an equation
If an approximation to the root 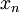 is already available then the next
approximation
is already available then the next
approximation
is calculated by requiring that
Using Taylors formula and assuming that 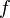 is differentiable we can
approximate the left hand side,
is differentiable we can
approximate the left hand side,
so that the new approximation is given by
This defines the iterative scheme for Newton-Raphson method and the solution if it exists, is the fixed point of
If we assume that
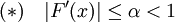
in some neighbourhood of the solution then
Thus condition (*) guarantees that 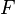 is contractive and the
Newton iterations will converge.
is contractive and the
Newton iterations will converge.

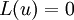
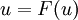
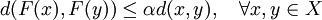
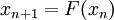

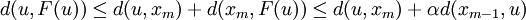

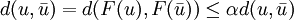

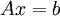
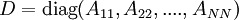
![x = D^{-1} [ b - (A-D)x]](/W/images/math/d/e/6/de6aeee7074774c4e466037a40efdd67.png)
![F(x) = D^{-1} [ b - (A-D)x]](/W/images/math/b/0/5/b0596f37d9fea4eb6c98519ce83409fb.png)
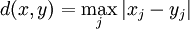
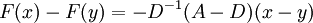
![[F(x) - F(y)]_j = \sum_{k \ne j} \frac{ A_{jk} }{ A_{jj}} (x_k - y_k)](/W/images/math/3/7/6/376f0c6fc023faf00f543eed006e9ea5.png)
![| [F(x) - F(y)]_j | \le \max_k | x_k - y_k | \sum_{k \ne j} \left|
\frac{ A_{jk} }{ A_{jj}} \right|](/W/images/math/4/7/4/474fb1606f1f2ee178dfc7ee4313bbe8.png)