Arbitrary polyhedral volume

(Difference between revisions)

Latest revision as of 06:18, 3 October 2005

The volume of arbitrary polyhedral can be calculated by using Green-Gauss Theorem.

$\int\limits_\Omega {div(\vec F)d\Omega = } \oint\limits_S {\vec F \bullet d\vec S}$

By choosing the function

$\vec F = \frac{{\left( {x\hat i + y\hat j + z\hat k} \right)}}{3}$

Where (x,y,z) are centroid of the surface enclosing the volume under consideration. As we have,

$div(\vec F) = 1$

Hence the volume can be calculated as:

$volume = \oint\limits_S {\vec F \bullet \hat ndS}$

where the normal of the surface pointing outwards is given by:

$\hat n = (n_x \hat i + n_y \hat j + n_z \hat k)$

Final expression could be written as

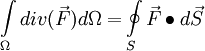
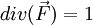
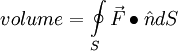
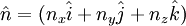
$volume = \frac{1}{3}\sum\limits_{faces} {\left[ {\left( {x \times n_x + y \times n_y + z \times n_z } \right) \bullet S} \right]}$

where S is magnitude of Surface Area.

@@ Line 36: / Line 36: @@
 where S is magnitude of Surface Area.
+----
+<i> Return to [[Numerical methods | Numerical Methods]] </i>