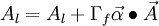Solution of Poisson's equation
From CFD-Wiki
(Difference between revisions)
| Line 25: | Line 25: | ||
D_{explicit} = \Gamma _f \left[ {\bar \nabla \phi \bullet \vec A - \left( {\bar \nabla \phi \bullet d\vec s} \right)\vec \alpha \bullet \vec A} \right] | D_{explicit} = \Gamma _f \left[ {\bar \nabla \phi \bullet \vec A - \left( {\bar \nabla \phi \bullet d\vec s} \right)\vec \alpha \bullet \vec A} \right] | ||
</math> <br> | </math> <br> | ||
| + | |||
| + | This gives us the coefficient of matrix as: | ||
| + | :<math> | ||
| + | A_l = A_l + \Gamma _f \vec \alpha \bullet \vec A | ||
| + | </math> <br> | ||
| + | |||
| + | :<math> | ||
| + | A_P = A_P - \Gamma _f \vec \alpha \bullet \vec A | ||
| + | </math> <br> | ||
| + | |||
| + | and for source matrix: <br> | ||
| + | <math> | ||
| + | S_U = S_U + q_\phi - D_{explicit} = S_U + q_\phi - \Gamma _f \left[ {\bar \nabla \phi \bullet \vec A - \left( {\bar \nabla \phi \bullet d\vec s} \right)\vec \alpha \bullet \vec A} \right] | ||
| + | |||
| + | </math> <br> | ||
| + | |||
| + | One the coefficient and source matrix is constructed, the system could be solved with the help of iterative solvers. | ||
Revision as of 06:12, 3 October 2005
Poisson equation occurs in many forms in CFD. Efficient and fast solution to Poisson equation is important aspect of CFD.
In CFD the Poisson equation occurs mainly in the form:
The solution
The left hand side can be discretised in the manner explained in section related to diffusive term . The diffusive term can be broken into two explicit and implicit parts.
We have, 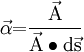
giving us the expression:
where 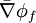 and
and 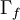 are suitable face averages.
are suitable face averages.
When broken into implicit and explicit parts
This gives us the coefficient of matrix as:
and for source matrix:
![S_U = S_U + q_\phi - D_{explicit} = S_U + q_\phi - \Gamma _f \left[ {\bar \nabla \phi \bullet \vec A - \left( {\bar \nabla \phi \bullet d\vec s} \right)\vec \alpha \bullet \vec A} \right]](/W/images/math/0/7/9/079149afed82462209a7ed984989c7ee.png)
One the coefficient and source matrix is constructed, the system could be solved with the help of iterative solvers.

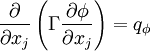
![D_f = \Gamma _f \nabla \phi _f \bullet {\rm{\vec A = }}\Gamma _{\rm{f}} \left[ {\left( {\phi _1 - \phi _0 } \right)\vec \alpha \bullet {\rm{\vec A + }}\bar \nabla \phi \bullet {\rm{\vec A - }}\left( {\bar \nabla \phi \bullet {\rm{d\vec s}}} \right)\vec \alpha \bullet {\rm{\vec A}}} \right]](/W/images/math/7/7/2/772b96059e9032fc07b25c0dee76db6c.png)
![D_{implicit} = \Gamma _{\rm{f}} \left[ {\left( {\phi _1 - \phi _0 } \right)\vec \alpha \bullet {\rm{\vec A }} } \right]](/W/images/math/e/b/6/eb6a1eedd86844e3b07754871a790a5e.png)
![D_{explicit} = \Gamma _f \left[ {\bar \nabla \phi \bullet \vec A - \left( {\bar \nabla \phi \bullet d\vec s} \right)\vec \alpha \bullet \vec A} \right]](/W/images/math/d/8/f/d8fe36fb5c721a8e4f2b149de57925fb.png)