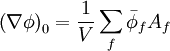Gradient computation
From CFD-Wiki
(Difference between revisions)
| Line 11: | Line 11: | ||
== Value at Face == | == Value at Face == | ||
| + | === Cell Based === | ||
There are many ways of estimating value of <math> \phi </math> at face. <br> | There are many ways of estimating value of <math> \phi </math> at face. <br> | ||
# Weighted interpolation: <math> \phi _f = w\phi _1 + \left( {1 - w} \right)\phi _0 </math> | # Weighted interpolation: <math> \phi _f = w\phi _1 + \left( {1 - w} \right)\phi _0 </math> | ||
#Arithmatic Average: <math> \phi _f = 0.5 \left( \phi _1 + \phi _0 \right) </math> | #Arithmatic Average: <math> \phi _f = 0.5 \left( \phi _1 + \phi _0 \right) </math> | ||
| + | |||
| + | ===Node Based === | ||
| + | |||
== Note == | == Note == | ||
The above mentioned gradients are sometimes called '''unlimited gradients''' since the face value obtained from them can exceed the bounding cell values. For this reason, for implementing higher order schemes, it becomes important to restrict them, so as not to introduce over and undershoot of variables. | The above mentioned gradients are sometimes called '''unlimited gradients''' since the face value obtained from them can exceed the bounding cell values. For this reason, for implementing higher order schemes, it becomes important to restrict them, so as not to introduce over and undershoot of variables. | ||
Revision as of 05:16, 3 October 2005
Contents |
Gradient Calculation
From Green-Gauss theorem:
Written in discrete form:
Value at Face
Cell Based
There are many ways of estimating value of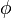 
at face.
- Weighted interpolation:
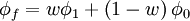
- Arithmatic Average:
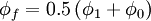
Node Based
Note
The above mentioned gradients are sometimes called unlimited gradients since the face value obtained from them can exceed the bounding cell values. For this reason, for implementing higher order schemes, it becomes important to restrict them, so as not to introduce over and undershoot of variables.
