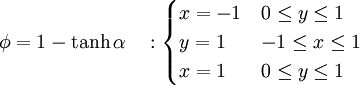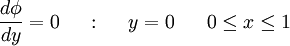Approximation Schemes for convective term - structured grids - Summary of Discretizations Schemes and examples
From CFD-Wiki
(→Pure convection of a scalar step by a rotating velocity field (Smith-Hutton problem)) |
(→Pure convection of a scalar step by a rotating velocity field (Smith-Hutton problem)) |
||
| Line 75: | Line 75: | ||
</td><td width="5%">(2)</td></tr></table> | </td><td width="5%">(2)</td></tr></table> | ||
| - | Thus | + | Thus <math>\boldsymbol{\phi}</math> is <math>\boldsymbol{0}</math> on <math>\boldsymbol{x\pm 1 }</math> and <math>\boldsymbol{y=1}</math>, and is <math>\boldsymbol{2}</math> at the origin. At the outlet a zero normal derivative is prescribed |
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
Revision as of 10:58, 30 September 2005
When we shall fill this page, I offer to make common identifications, because in different issues was used different notation.
Also we beg everybody to help me with original works. Later I shall write, what is necessary. If anyone have literature connected with convective schemes, please drop me a line.
We shall be very glad and grateful to hear any critical suggestion (please drop a few lines at Wiki Forum)
It is just a skeleton, but we hope that it will be developed into the good thing
Contents |
Discretizations Schemes Estimation of order
Discretizations Schemes Estimation of error
Selection advice
Comparison of Discretizations Schemes
Numerical examples
Pure convection of a scalar step by a rotating velocity field (Smith-Hutton problem)
R.M.Smith and A.G.Hutton (1982), "The numerical treatment of advection: A performance comparison of current methods", Numerical Heat Transfer, Vol. 5, p439.
This was the test problem devised for evaluating a range of numerical models of convection at the third meeting of the International Association for Hydraulic Research Working Group on Refined Modelling of flow
Sometimes it was used scalar profile with a discontinuity at 
We shall use here smooth inlet profile
This is a simple problem with a strong discontinuity in a scalar profile and flow that is not parallel to the boundaries of the domain being tested. As such it should reveal the poor convergence of the first order schemes, which exhibit false diffusion on flow that is not parallel to the grid, whilst the sharp gradient should generate oscillations in the solutions generated using the second and third order schemes.
The steady transport equation is solved in the region  \ , \
\ , \  , with the streamfunction being specified as
, with the streamfunction being specified as
|
| (1) |
which is shown in figure below. This streamfunction gives a velocity field of
|
| (1) |
|
| (1) |
The scalar 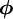 is solved over the domain, with the value of
is solved over the domain, with the value of 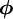 being prescribed at the inlet and on the left, right and top boundaries, whilst on the outlet the derivative of
being prescribed at the inlet and on the left, right and top boundaries, whilst on the outlet the derivative of 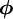 normal to the boudary is set to zero. The inlet profile is given as
normal to the boudary is set to zero. The inlet profile is given as
|
| (1) |
where  is a parameter which defines the sharpness of the inlet profile. The outer boundaries are prescribed as
is a parameter which defines the sharpness of the inlet profile. The outer boundaries are prescribed as
|
| (2) |
Thus 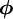 is
is 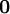 on
on 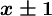 and
and 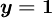 , and is
, and is 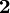 at the origin. At the outlet a zero normal derivative is prescribed
at the origin. At the outlet a zero normal derivative is prescribed
|
| (2) |
Square Lid-driven cavity flow
Example code for solving Smith-Hutton problem
Dear friends
It's just a scrap. Later I'll correct it, although it's a complete working code
Michail
Sample code for solving Smith-Hutton test - Fortran 90
It's a results, obtained using this code (UDS and HLPA schemes)
Below it's cleary seen the numerical diffusion impact, comparing the contour fields obtaining using the UDS and HLPA. A bit later we shall place here a solution gained with QUICK scheme, and it will be seen the osscilations.

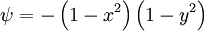
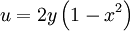

![\phi = 1 + \tanh \left[ \alpha \left( 2x + 1 \right) \right] \ \ \ : \ \ \ y=0 \ \ \ -1 \leq x \leq 0](/W/images/math/1/2/5/1258744eacb251f22686767b254b6085.png)