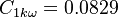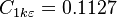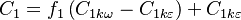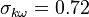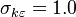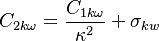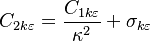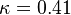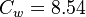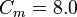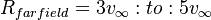Wray-Agarwal(WA) Turbulence Model
From CFD-Wiki
(Difference between revisions)
Lin.zhenghao (Talk | contribs) (Created page with "== Introduction == The WA 2017m model is a one-equation model that was derived from two-equation <math>k-\omega</math> closure. It combines the most desirable characteristics of ...") |
(→Introduction) |
||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| - | The WA 2017m model is a one-equation model that was derived from two-equation <math>k-\omega</math> closure. It combines the most desirable characteristics of the one-equation <math>k-\epsilon</math> model and one-equation <math>k-\omega</math> model, analogous to the SST <math>k-\omega</math> model which combines best features of two-equation <math>k-\epsilon</math> and <math>k-\omega</math> models. | + | The Wray-Agarwal (WA 2017m) model is a one-equation linear eddy viscosity model that was derived from two-equation <math>k-\omega</math> closure. It combines the most desirable characteristics of the one-equation <math>k-\epsilon</math> model and one-equation <math>k-\omega</math> model, analogous to the SST <math>k-\omega</math> model which combines best features of two-equation <math>k-\epsilon</math> and <math>k-\omega</math> models. |
==WA Model== | ==WA Model== | ||
Revision as of 21:15, 22 January 2021
Contents |
Introduction
The Wray-Agarwal (WA 2017m) model is a one-equation linear eddy viscosity model that was derived from two-equation 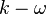 closure. It combines the most desirable characteristics of the one-equation
closure. It combines the most desirable characteristics of the one-equation 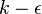 model and one-equation
model and one-equation 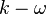 model, analogous to the SST
model, analogous to the SST 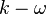 model which combines best features of two-equation
model which combines best features of two-equation 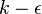 and
and 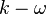 models.
models.
WA Model
The turbulent eddy viscosity is given by:
The model solves for the variable 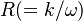 using the following equation:
using the following equation:
Where:
and d is the minimum distance to the nearest wall.
The model constants are:
Boundary Conditions
Solid smooth wall:
Freestream:
References
- X. Han, T. J. Wray, and R. K. Agarwal. (2017), "Application of a New DES Model Based on Wray-Agarwal Turbulence Model for Simulation of Wall-Bounded Flows with Separation", AIAA Paper 2017-3966, June 2017.

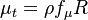
![\begin{matrix}
\frac{\partial R}{\partial t}+\frac{\partial u_{j} R}{\partial x_{j}}=& \frac{\partial}{\partial x_{j}}\left[\left(\sigma_{R} R+v\right) \frac{\partial R}{\partial x_{j}}\right]+C_{1} R S+f_{1} C_{2 k \omega} \frac{R}{S} \frac{\partial R}{\partial x_{j}} \frac{\partial S}{\partial x_{j}}\\
&-\left(1-f_{1}\right) \min \left[C_{2 k \varepsilon} R^{2}\left(\frac{\frac{\partial S}{\partial x_{j}} \frac{\partial S}{\partial x_{j}}}{S^{2}}\right), C_{m} \frac{\partial R}{\partial x_{j}} \frac{\partial R}{\partial x_{j}}\right]
\end{matrix}](/W/images/math/b/f/7/bf7b8d748dcdc15f608c08bf0d09f667.png)
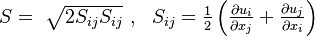
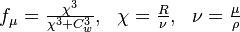
![\begin{matrix}
{{f}_{1}}=\min \left( \tanh \left( arg_{1}^{4} \right),0.9 \right),~~ar{{g}_{1}}=\frac{1+\frac{d\sqrt{RS}}{\nu }}{1+{{\left[ \frac{max\left( d\sqrt{RS},1.5R \right)}{20\nu } \right]}^{2}}}
\end{matrix}](/W/images/math/e/e/0/ee05356999b3ac7c223400c85388da14.png)