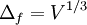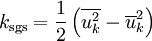Kinetic energy subgrid-scale model
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| - | <math> k_{\rm sgs} = \frac{1}{2}\left(\overline{u_k^2} - \overline{u}_k^2 \right) </math> | + | The subgrid-scale kinetic energy is defined as <br> |
| + | :<math> k_{\rm sgs} = \frac{1}{2}\left(\overline{u_k^2} - \overline{u}_k^2 \right) </math> | ||
| + | |||
| + | |||
| + | The subgrid-scale stress can then be written as <br> | ||
| + | <math> \tau_{ij} - \frac{2}{3} k_{\rm sgs} \delta_{ij} =-2 C_k k_{\rm sgs}^{1/2} \Delta_f \overline{S}_{ij} </math> <br> | ||
| + | this gives us the transport equation for subgrid-scale kinetic energy <br> | ||
| + | <math> \frac{\partial \overline k_{\rm sgs}}{\partial t} + \frac{\partial \overline u_{j} \overline k_{sgs}} {\partial x_{j}} = - \tau_{ij} \frac{\partial \overline u_{i}}{\partial x_{j}} - C_{\varepsilon} \frac{k_{\rm sgs}^{3/2}}{\Delta_f} + \frac{\partial}{\partial x_{j}} \left( \frac{\mu_t}{\sigma_k} \frac{\partial k_{\rm sgs}}{\partial x_{j}} \right) </math> | ||
| + | |||
| + | |||
| + | |||
| + | The subgrid-scale eddy viscosity,<math> \mu_{t} </math>, is computed using <math> k_{\rm sgs} </math> as | ||
| + | |||
| + | |||
| + | <math> \mu_{t} = C_k k_{\rm sgs}^{1/2} \Delta_f </math> | ||
| + | |||
| + | Where the filter-size computed from: <br> | ||
| + | <math> \Delta_f = V^{1/3} </math> | ||
Revision as of 23:43, 18 September 2005
The subgrid-scale kinetic energy is defined as
The subgrid-scale stress can then be written as
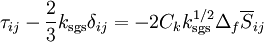
this gives us the transport equation for subgrid-scale kinetic energy
The subgrid-scale eddy viscosity,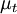
, is computed using 
as
Where the filter-size computed from:
