Realisable k-epsilon model
From CFD-Wiki
(Difference between revisions)
| Line 6: | Line 6: | ||
:<math> \frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_j} (\rho \epsilon u_j) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_{\epsilon}}\right) \frac{\partial \epsilon}{\partial x_j} \right ] + \rho \, C_1 S \epsilon - \rho \, C_2 \frac{{\epsilon}^2} {k + \sqrt{\nu \epsilon}} + C_{1 \epsilon}\frac{\epsilon}{k} C_{3 \epsilon} P_b + S_{\epsilon} </math> | :<math> \frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_j} (\rho \epsilon u_j) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_{\epsilon}}\right) \frac{\partial \epsilon}{\partial x_j} \right ] + \rho \, C_1 S \epsilon - \rho \, C_2 \frac{{\epsilon}^2} {k + \sqrt{\nu \epsilon}} + C_{1 \epsilon}\frac{\epsilon}{k} C_{3 \epsilon} P_b + S_{\epsilon} </math> | ||
| + | |||
| + | Where <br> | ||
| + | |||
| + | <math> C_1 = \max\left[0.43, \frac{\eta}{\eta + 5}\right] , \;\;\;\;\; \eta = S \frac{k}{\epsilon}, \;\;\;\;\; S =\sqrt{2 S_{ij} S_{ij}} </math> <br> | ||
| + | |||
| + | In these equations, <math> P_k </math> represents the generation of turbulence kinetic energy due to the mean velocity gradients, calculated in same manner as standard k-epsilon model. <math> P_b </math> is the generation of turbulence kinetic energy due to buoyancy, calculated in same way as standard k-epsilon model. | ||
Revision as of 22:52, 18 September 2005
Transport Equations
Where
![C_1 = \max\left[0.43, \frac{\eta}{\eta + 5}\right] , \;\;\;\;\; \eta = S \frac{k}{\epsilon}, \;\;\;\;\; S =\sqrt{2 S_{ij} S_{ij}}](/W/images/math/1/9/3/193f62d995a6b0190d41325b612bf336.png)
In these equations, 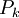 represents the generation of turbulence kinetic energy due to the mean velocity gradients, calculated in same manner as standard k-epsilon model.
represents the generation of turbulence kinetic energy due to the mean velocity gradients, calculated in same manner as standard k-epsilon model. 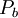 is the generation of turbulence kinetic energy due to buoyancy, calculated in same way as standard k-epsilon model.
is the generation of turbulence kinetic energy due to buoyancy, calculated in same way as standard k-epsilon model.

![\frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_j} (\rho k u_j) = \frac{\partial}{\partial x_j} \left [ \left(\mu + \frac{\mu_t}{\sigma_k}\right) \frac{\partial k} {\partial x_j} \right ] + P_k + P_b - \rho \epsilon - Y_M + S_k](/W/images/math/0/0/4/004f9597d5f640c6152d7ee7ec2af16a.png)
![\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_j} (\rho \epsilon u_j) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_{\epsilon}}\right) \frac{\partial \epsilon}{\partial x_j} \right ] + \rho \, C_1 S \epsilon - \rho \, C_2 \frac{{\epsilon}^2} {k + \sqrt{\nu \epsilon}} + C_{1 \epsilon}\frac{\epsilon}{k} C_{3 \epsilon} P_b + S_{\epsilon}](/W/images/math/9/e/1/9e195cf17f086a6a1ad3914571b491ba.png)