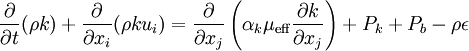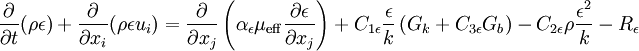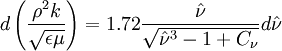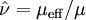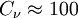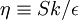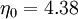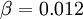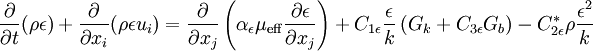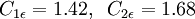RNG k-epsilon model
From CFD-Wiki
(Difference between revisions)
(→adding basic equations) |
|||
| Line 1: | Line 1: | ||
== RNG k-epsilon model == | == RNG k-epsilon model == | ||
| - | Transport equations for k and \epsilon are | + | Transport equations for k and <math>\epsilon</math> are |
:<math> | :<math> | ||
| Line 10: | Line 10: | ||
</math> | </math> | ||
| - | + | == Turbulent viscosity is modelled as== | |
:<math> | :<math> | ||
d \left(\frac{\rho^2 k}{\sqrt{\epsilon \mu}} \right) = 1.72 \frac{\hat{\nu}}{\sqrt{{\hat{\nu}}^3-1+C_\nu}} d{\hat{\nu}} | d \left(\frac{\rho^2 k}{\sqrt{\epsilon \mu}} \right) = 1.72 \frac{\hat{\nu}}{\sqrt{{\hat{\nu}}^3-1+C_\nu}} d{\hat{\nu}} | ||
| Line 24: | Line 24: | ||
</math> | </math> | ||
| - | + | == Term <math> R_{\epsilon} </math> == | |
| + | The term <math> R_{\epsilon} </math> is modelled as <br> | ||
:<math> | :<math> | ||
R_{\epsilon} = \frac{C_\mu \rho \eta^3 (1-\eta/\eta_0)}{1+\beta\eta^3} \frac{\epsilon^2}{k} | R_{\epsilon} = \frac{C_\mu \rho \eta^3 (1-\eta/\eta_0)}{1+\beta\eta^3} \frac{\epsilon^2}{k} | ||
| Line 41: | Line 42: | ||
</math> | </math> | ||
| - | + | The transport equation for <math>\epsilon</math> can be re-written as: <br> | |
:<math> | :<math> | ||
\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left(\alpha_{\epsilon} \mu_{\rm eff} \frac{\partial \epsilon}{\partial x_j}\right) + C_{1 \epsilon}\frac{\epsilon}{k} \left( G_k + C_{3 \epsilon} G_b \right) - C_{2\epsilon}^* \rho \frac{\epsilon^2}{k} | \frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left(\alpha_{\epsilon} \mu_{\rm eff} \frac{\partial \epsilon}{\partial x_j}\right) + C_{1 \epsilon}\frac{\epsilon}{k} \left( G_k + C_{3 \epsilon} G_b \right) - C_{2\epsilon}^* \rho \frac{\epsilon^2}{k} | ||
Revision as of 13:13, 14 September 2005
RNG k-epsilon model
Transport equations for k and  are
are
Turbulent viscosity is modelled as
and
Term 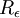
The term 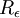 is modelled as
is modelled as
The transport equation for  can be re-written as:
can be re-written as: