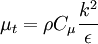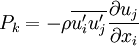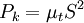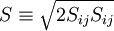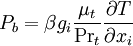Standard k-epsilon model
From CFD-Wiki
(Difference between revisions)
| Line 2: | Line 2: | ||
For k <br> | For k <br> | ||
| - | <math> \frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k </math> | + | :<math> \frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k </math> |
<br> | <br> | ||
| Line 8: | Line 8: | ||
<br> | <br> | ||
| - | <math> | + | :<math> |
\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left[\left(\mu + \frac{\mu_t}{\sigma_{\epsilon}} \right) \frac{\partial \epsilon}{\partial x_j} \right] + C_{1 \epsilon}\frac{\epsilon}{k} \left( P_k + C_{3 \epsilon} P_b \right) - C_{2 \epsilon} \rho \frac{\epsilon^2}{k} + S_{\epsilon} | \frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left[\left(\mu + \frac{\mu_t}{\sigma_{\epsilon}} \right) \frac{\partial \epsilon}{\partial x_j} \right] + C_{1 \epsilon}\frac{\epsilon}{k} \left( P_k + C_{3 \epsilon} P_b \right) - C_{2 \epsilon} \rho \frac{\epsilon^2}{k} + S_{\epsilon} | ||
| - | + | </math> | |
| - | + | ||
== Modeling turbulent viscosity == | == Modeling turbulent viscosity == | ||
Turbulent viscosity is modelled as: <br> | Turbulent viscosity is modelled as: <br> | ||
| - | <math> | + | :<math> |
\mu_t = \rho C_{\mu} \frac{k^2}{\epsilon} | \mu_t = \rho C_{\mu} \frac{k^2}{\epsilon} | ||
</math> | </math> | ||
| Line 25: | Line 24: | ||
== Production of k == | == Production of k == | ||
| - | <math> | + | :<math> |
P_k = - \rho \overline{u'_i u'_j} \frac{\partial u_j}{\partial x_i} | P_k = - \rho \overline{u'_i u'_j} \frac{\partial u_j}{\partial x_i} | ||
</math> | </math> | ||
<br> | <br> | ||
| - | <math> P_k = \mu_t S^2 </math> | + | :<math> P_k = \mu_t S^2 </math> |
Where <math> S </math> is the modulus of the mean rate-of-strain tensor, defined as : <br> | Where <math> S </math> is the modulus of the mean rate-of-strain tensor, defined as : <br> | ||
| - | <math> | + | :<math> |
S \equiv \sqrt{2S_{ij} S_{ij}} | S \equiv \sqrt{2S_{ij} S_{ij}} | ||
</math> | </math> | ||
| Line 38: | Line 37: | ||
== Effect of Bouyancy == | == Effect of Bouyancy == | ||
| - | <math> | + | :<math> |
P_b = \beta g_i \frac{\mu_t}{{\rm Pr}_t} \frac{\partial T}{\partial x_i} | P_b = \beta g_i \frac{\mu_t}{{\rm Pr}_t} \frac{\partial T}{\partial x_i} | ||
</math> | </math> | ||
| Line 47: | Line 46: | ||
The coefficient of thermal expansion, <math> \beta </math> , is defined as <br> | The coefficient of thermal expansion, <math> \beta </math> , is defined as <br> | ||
| - | <math> | + | :<math> |
\beta = - \frac{1}{\rho} \left(\frac{\partial \rho}{\partial T}\right)_p | \beta = - \frac{1}{\rho} \left(\frac{\partial \rho}{\partial T}\right)_p | ||
</math> | </math> | ||
| Line 53: | Line 52: | ||
== Model Constants == | == Model Constants == | ||
| - | <math> | + | :<math> |
C_{1 \epsilon} = 1.44, \;\; C_{2 \epsilon} = 1.92, \;\; C_{\mu} = 0.09, \;\; \sigma_k = 1.0, \;\; \sigma_{\epsilon} = 1.3 | C_{1 \epsilon} = 1.44, \;\; C_{2 \epsilon} = 1.92, \;\; C_{\mu} = 0.09, \;\; \sigma_k = 1.0, \;\; \sigma_{\epsilon} = 1.3 | ||
</math> | </math> | ||
Revision as of 08:09, 14 September 2005
Contents |
Transport Equations for standard k-epsilon model
For k
For dissipation 
Modeling turbulent viscosity
Turbulent viscosity is modelled as:
Production of k
Where 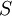 is the modulus of the mean rate-of-strain tensor, defined as :
is the modulus of the mean rate-of-strain tensor, defined as :
Effect of Bouyancy
where Prt is the turbulent Prandtl number for energy and gi is the component of the gravitational vector in the ith direction. For the standard and realizable - models, the default value of Prt is 0.85.
The coefficient of thermal expansion, 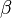 , is defined as
, is defined as

![\frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k](/W/images/math/0/3/3/03313e8802538459d0a202c34efc1274.png)
![\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left[\left(\mu + \frac{\mu_t}{\sigma_{\epsilon}} \right) \frac{\partial \epsilon}{\partial x_j} \right] + C_{1 \epsilon}\frac{\epsilon}{k} \left( P_k + C_{3 \epsilon} P_b \right) - C_{2 \epsilon} \rho \frac{\epsilon^2}{k} + S_{\epsilon}](/W/images/math/0/6/c/06ca9efd2f29b3816707de0452572c77.png)