Standard k-epsilon model
From CFD-Wiki
(Difference between revisions)
| Line 1: | Line 1: | ||
| + | == Transport Equation for standard k-epsilon model == | ||
| + | |||
| + | For k <br> | ||
<math> \frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k </math> | <math> \frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k </math> | ||
| - | |||
| + | <br> | ||
| + | For dissipation <math> \epsilon </math> | ||
<br> | <br> | ||
| Line 9: | Line 13: | ||
</math> | </math> | ||
| + | == Modeling turbulent viscosity == | ||
| + | Turbulent viscosity is modelled as: <br> | ||
<math> | <math> | ||
\mu_t = \rho C_{\mu} \frac{k^2}{\epsilon} | \mu_t = \rho C_{\mu} \frac{k^2}{\epsilon} | ||
</math> | </math> | ||
| + | <br> | ||
| + | |||
| + | == Model Constants == | ||
<math> | <math> | ||
C_{1 \epsilon} = 1.44, \;\; C_{2 \epsilon} = 1.92, \;\; C_{\mu} = 0.09, \;\; \sigma_k = 1.0, \;\; \sigma_{\epsilon} = 1.3 | C_{1 \epsilon} = 1.44, \;\; C_{2 \epsilon} = 1.92, \;\; C_{\mu} = 0.09, \;\; \sigma_k = 1.0, \;\; \sigma_{\epsilon} = 1.3 | ||
</math> | </math> | ||
Revision as of 00:14, 14 September 2005
Transport Equation for standard k-epsilon model
For k
![\frac{\partial}{\partial t} (\rho k) + \frac{\partial}{\partial x_i} (\rho k u_i) = \frac{\partial}{\partial x_j} \left[ \left(\mu + \frac{\mu_t}{\sigma_k} \right) \frac{\partial k}{\partial x_j}\right] + P_k + P_b - \rho \epsilon - Y_M + S_k](/W/images/math/0/3/3/03313e8802538459d0a202c34efc1274.png)
For dissipation 
![\frac{\partial}{\partial t} (\rho \epsilon) + \frac{\partial}{\partial x_i} (\rho \epsilon u_i) = \frac{\partial}{\partial x_j} \left[\left(\mu + \frac{\mu_t}{\sigma_{\epsilon}} \right) \frac{\partial \epsilon}{\partial x_j} \right] + C_{1 \epsilon}\frac{\epsilon}{k} \left( P_k + C_{3 \epsilon} P_b \right) - C_{2 \epsilon} \rho \frac{\epsilon^2}{k} + S_{\epsilon}](/W/images/math/0/6/c/06ca9efd2f29b3816707de0452572c77.png)
Modeling turbulent viscosity
Turbulent viscosity is modelled as:
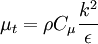
Model Constants

