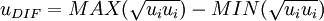Baldwin-Lomax model
From CFD-Wiki
| Line 1: | Line 1: | ||
| - | The Baldwin-Lomax model is a two-layer algebraic model which gives <math>\mu_t</math> as a function of the local boundary layer velocity profile | + | The Baldwin-Lomax model is a two-layer algebraic model which gives the eddy-viscosity <math>\mu_t</math> as a function of the local boundary layer velocity profile: |
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
:<math> | :<math> | ||
| - | \mu_t = | + | \mu_t = |
| - | \begin{ | + | \begin{cases} |
| - | {\mu_t}_{inner} & y \ | + | {\mu_t}_{inner} & \mbox{if } y \le y_{crossover} \\ |
| - | {\mu_t}_{outer} & y > y_{crossover} | + | {\mu_t}_{outer} & \mbox{if} y > y_{crossover} |
| - | \end{ | + | \end{cases} |
| - | + | ||
</math></td><td width="5%">(1)</td></tr></table> | </math></td><td width="5%">(1)</td></tr></table> | ||
| Line 29: | Line 28: | ||
<table width="100%"><tr><td> | <table width="100%"><tr><td> | ||
:<math> | :<math> | ||
| - | + | l = k y \left( 1 - e^{\frac{-y^+}{A^+}} \right) | |
| - | l = k y \left( 1 - | + | |
</math></td><td width="5%">(4)</td></tr></table> | </math></td><td width="5%">(4)</td></tr></table> | ||
| Line 60: | Line 58: | ||
F_{WAKE} = MIN \left( y_{MAX} \, F_{MAX} \,\,;\,\, | F_{WAKE} = MIN \left( y_{MAX} \, F_{MAX} \,\,;\,\, | ||
C_{WK} \, y_{MAX} \, \frac{u^2_{DIF}}{F_{MAX}} \right) | C_{WK} \, y_{MAX} \, \frac{u^2_{DIF}}{F_{MAX}} \right) | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(8)</td></tr></table> |
<math>y_{MAX}</math> and <math>F_{MAX}</math> are determined from the maximum of the function: | <math>y_{MAX}</math> and <math>F_{MAX}</math> are determined from the maximum of the function: | ||
| - | <table width="100%"><tr><td>:<math> | + | <table width="100%"><tr><td> |
| - | + | :<math> | |
| - | F(y) = y \left| \Omega \right| \left(1- | + | F(y) = y \left| \Omega \right| \left(1-e^{\frac{-y^+}{A^+}} \right) |
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(9)</td></tr></table> |
<math>F_{KLEB}</math> is the intermittency factor given by: | <math>F_{KLEB}</math> is the intermittency factor given by: | ||
| - | <table width="100%"><tr><td>:<math> | + | <table width="100%"><tr><td> |
| + | :<math> | ||
F_{KLEB}(y) = \left[1 + 5.5 \left( \frac{y \, C_{KLEB}}{y_{MAX}} \right)^6 | F_{KLEB}(y) = \left[1 + 5.5 \left( \frac{y \, C_{KLEB}}{y_{MAX}} \right)^6 | ||
\right]^{-1} | \right]^{-1} | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(10)</td></tr></table> |
<math>u_{DIF}</math> is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero. | <math>u_{DIF}</math> is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero. | ||
| - | <table width="100%"><tr><td>:<math> | + | <table width="100%"><tr><td> |
| + | :<math> | ||
u_{DIF} = MAX(\sqrt{u_i u_i}) - MIN(\sqrt{u_i u_i}) | u_{DIF} = MAX(\sqrt{u_i u_i}) - MIN(\sqrt{u_i u_i}) | ||
| - | </math></td><td width="5%">( | + | </math></td><td width="5%">(11)</td></tr></table> |
| + | |||
| + | |||
| + | == Model constants == | ||
| + | |||
| + | The table below gives the model constants present in the formulas above. Note that <math>k</math> is a constant, and not the turbulence energy, as in other sections. It should also be pointed out that when using the Baldwin-Lomax model the turbulence energy, <math>k</math>, present in the governing equations, is set to zero. | ||
| - | + | <table cellpadding="5" cellspacing="1" border="1"> | |
| - | + | <tr> | |
| - | + | <td><math>A^+</math></td> | |
| - | + | <td><math>C_{CP}</math></td> | |
| - | <math>A^+<math> | + | <td><math>C_{KLEB}</math></td> |
| - | + | <td><math>C_{WK}</math></td> | |
| - | 26 | + | <td><math>k</math></td> |
| - | + | <td><math>K</math></td> | |
| - | + | </tr> | |
| - | + | <tr> | |
| - | + | <td>26</td> | |
| - | + | <td>1.6</td> | |
| + | <td>0.3</td> | ||
| + | <td>0.25</td> | ||
| + | <td>0.4</td> | ||
| + | <td>0.0168</td> | ||
| + | </tr> | ||
| + | </table> | ||
| - | |||
== References == | == References == | ||
| - | ''Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows'' by B. S. Baldwin and H. Lomax, AIAA Paper 78-257, 1978 | + | * ''Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows'' by B. S. Baldwin and H. Lomax, AIAA Paper 78-257, 1978 |
Revision as of 12:28, 8 September 2005
The Baldwin-Lomax model is a two-layer algebraic model which gives the eddy-viscosity 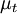 as a function of the local boundary layer velocity profile:
as a function of the local boundary layer velocity profile:
|
| (1) |
Where 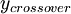 is the smallest distance from the surface where
is the smallest distance from the surface where 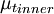 is equal to
is equal to 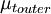 :
:
|
| (2) |
The inner region is given by the Prandtl - Van Driest formula:
|
| (3) |
Where
|
| (4) |
|
| (5) |
|
| (6) |
The outer region is given by:
|
| (7) |
Where
|
| (8) |
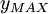 and
and 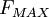 are determined from the maximum of the function:
are determined from the maximum of the function:
|
| (9) |
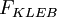 is the intermittency factor given by:
is the intermittency factor given by:
|
| (10) |
 is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
is the difference between maximum and minimum speed in the profile. For boundary layers the minimum is always set to zero.
|
| (11) |
Model constants
The table below gives the model constants present in the formulas above. Note that 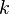 is a constant, and not the turbulence energy, as in other sections. It should also be pointed out that when using the Baldwin-Lomax model the turbulence energy,
is a constant, and not the turbulence energy, as in other sections. It should also be pointed out that when using the Baldwin-Lomax model the turbulence energy, 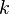 , present in the governing equations, is set to zero.
, present in the governing equations, is set to zero.
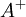 |
 |
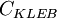 |
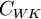 |
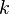 |
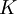 |
| 26 | 1.6 | 0.3 | 0.25 | 0.4 | 0.0168 |
References
- Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows by B. S. Baldwin and H. Lomax, AIAA Paper 78-257, 1978

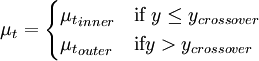
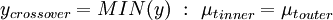
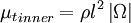
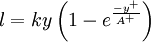

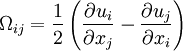
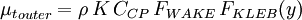
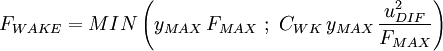
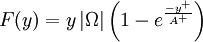
![F_{KLEB}(y) = \left[1 + 5.5 \left( \frac{y \, C_{KLEB}}{y_{MAX}} \right)^6
\right]^{-1}](/W/images/math/9/b/d/9bde77641b7e232fa3e083d3e59795c4.png)