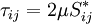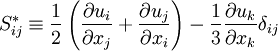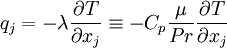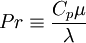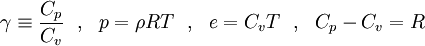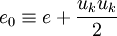Navier-Stokes equations
From CFD-Wiki
(→External Links) |
|||
| Line 104: | Line 104: | ||
*[http://www.navier-stokes.net Navier-Stokes.net] | *[http://www.navier-stokes.net Navier-Stokes.net] | ||
*[http://scienceworld.wolfram.com/physics/Navier-StokesEquations.html Navier-Stokes equations at mathworld.com] | *[http://scienceworld.wolfram.com/physics/Navier-StokesEquations.html Navier-Stokes equations at mathworld.com] | ||
| - | *[http://www.claymath.org/millennium/Navier-Stokes_Equations/ | + | *[http://www.claymath.org/millennium/Navier-Stokes_Equations/ Millenium Problem] |
Revision as of 10:08, 8 September 2005
The Navier-Stokes equations are the basic governing equations for a viscous, heat conducting fluid. It is a vector equation obtained by applying Newtons Law of Motion to a fluid element and is also called the momentum equation. It is supplemented by the mass conservation equation, also called continuity equation and the energy equation. Usually, the term Navier-Stokes equations is used to refer to all of these equations.
The instantaneous continuity equation (1), momentum equation (2) and energy equation (3) for a compressible fluid can be written as:
|
| (1) |
|
| (2) |
|
| (3) |
![\frac{\partial \rho}{\partial t} +
\frac{\partial}{\partial x_j}\left[ \rho u_j \right] = 0](/W/images/math/0/7/1/071e4f5508fd336ddad848551ce3188e.png)
![\frac{\partial}{\partial t}\left( \rho u_i \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_i u_j + p \delta_{ij} - \tau_{ji} \right] = 0](/W/images/math/6/f/c/6fc8041faa4be98ee72ec1e670fb22c7.png)
![\frac{\partial}{\partial t}\left( \rho e_0 \right) +
\frac{\partial}{\partial x_j}
\left[ \rho u_j e_0 + u_j p + q_j - u_i \tau_{ij} \right] = 0](/W/images/math/8/1/7/8176cdf87a72617542883cbbeafc50cc.png)
For a Newtonian fluid, assuming Stokes Law for mono-atomic gases, the viscous stress is given by:
|
| (4) |
Where the trace-less viscous strain-rate is defined by:
|
| (5) |
The heat-flux,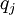 
, is given by Fourier's law:
|
| (6) |
Where the laminar Prandtl number 
is defined by:
|
| (7) |
To close these equations it is also necessary to specify an equation of state. Assuming a calorically perfect gas the following relations are valid:
|
| (8) |
Where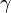 
, 
, 
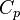and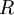 
are constant.
The total energy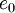 
is defined by:
|
| (9) |
Note that the corresponding expression (15) for Favre averaged turbulent flows contains an extra term related to the turbulent energy.
Equations (1)-(9), supplemented with gas data for , ,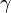 
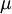and perhaps 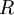, form a closed set of partial differential equations, and need only be complemented with boundary conditions.
