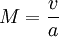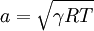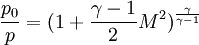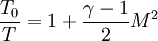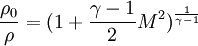Isentropic flow relations
From CFD-Wiki
(Difference between revisions)
| Line 4: | Line 4: | ||
<math>\frac{p_0}{p} = (\frac{T_0}{T})^\frac{\gamma}{\gamma - 1}</math> | <math>\frac{p_0}{p} = (\frac{T_0}{T})^\frac{\gamma}{\gamma - 1}</math> | ||
| - | |||
| - | |||
<math>\frac{p_0}{p}=(1+\frac{\gamma-1}{2}M^2)^{\frac{\gamma}{\gamma-1}}</math> | <math>\frac{p_0}{p}=(1+\frac{\gamma-1}{2}M^2)^{\frac{\gamma}{\gamma-1}}</math> | ||
| + | |||
| + | <math>\frac{T_0}{T}=1+\frac{\gamma-1}{2}M^2</math> | ||
<math>\frac{\rho_0}{\rho}=(1+\frac{\gamma-1}{2}M^2)^{\frac{1}{\gamma-1}}</math> | <math>\frac{\rho_0}{\rho}=(1+\frac{\gamma-1}{2}M^2)^{\frac{1}{\gamma-1}}</math> | ||
| - | <math>\frac{A}{A*}=(\frac{\gamma+1}{2})^{\frac{-\gamma+1}{2(\gamma-1)}}*(1+\frac{\gamma-1}{2}M^2)^{\frac{\gamma+1}{2(\gamma-1)}} | + | <math>\frac{A}{A*}=\frac{1}{M}*(\frac{\gamma+1}{2})^{\frac{-\gamma+1}{2(\gamma-1)}}*(1+\frac{\gamma-1}{2}M^2)^{\frac{\gamma+1}{2(\gamma-1)}}</math> |
Revision as of 21:39, 3 September 2005