A roughness-dependent model

(Difference between revisions)

Revision as of 15:28, 19 June 2007

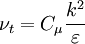$\nu _t = C_{\mu} {{k^2 } \over \varepsilon }$

(1)

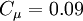
where: $C_{\mu} = 0.09$

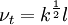$\nu _t = k^{{1 \over 2}} l$

(2)

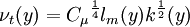$\nu _t(y) = {C_{\mu}}^{{1 \over 4}} l_m(y) k^{{1 \over 2}}(y)$

(3)

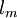$l_m$ is the mixing length.

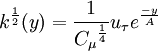$k^{{1 \over 2}}(y) = {1 \over {C_{\mu}}^{{1 \over 4}}} u_\tau e^{\frac{-y}{A}}$

(4)

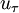$u_\tau$ is the shear velocity and 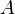$A$ a model parameter.

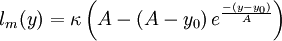$l_m(y) = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right)$

(5)

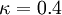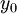$\kappa = 0.4$ , $y_0$ is the hydrodynamic roughness

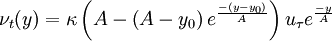$\nu _t(y) = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right) u_\tau e^{\frac{-y}{A}}$

(6)

for a smooth wall (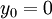 $y_0 = 0$ ):

$\nu _t(y) = \kappa A \left( 1 - e^{\frac{-y}{A}} \right) u_\tau e^{\frac{-y}{A}}$

(6)

Absi, R. (2006), "A roughness and time dependent mixing length equation", Journal of Hydraulic, Coastal and Environmental Engineering, Japan Society of Civil Engineers, (Doboku Gakkai Ronbunshuu B), Vol. 62, No. 4, pp.437-446.

This article is a stub, a short article which needs to be improved. You can help by expanding it.

@@ Line 38: / Line 38: @@
 <math>
 \nu _t(y)  = \kappa \left( A - \left(A - y_0\right) e^{\frac{-(y-y_0)}{A}} \right)
+ u_\tau  e^{\frac{-y}{A}}
+</math></td><td width="5%">(6)</td></tr></table>
+for a smooth wall (<math>y_0 = 0</math>):
+<table width="70%"><tr><td>
+<math>
+\nu _t(y)  = \kappa  A  \left( 1 - e^{\frac{-y}{A}} \right)
   u_\tau  e^{\frac{-y}{A}}
 </math></td><td width="5%">(6)</td></tr></table>