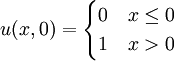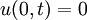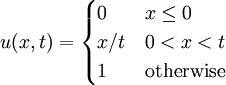Non linear wave propagation
From CFD-Wiki
(Difference between revisions)
(fixed up some formulas) |
|||
| Line 2: | Line 2: | ||
:<math> \frac{\partial u}{\partial t}+ u \frac{\partial u}{\partial x}=0 | :<math> \frac{\partial u}{\partial t}+ u \frac{\partial u}{\partial x}=0 | ||
</math> | </math> | ||
| + | |||
== Domain == | == Domain == | ||
| - | x | + | :<math>x \in \left[-5,10\right]</math> |
| + | |||
== Initial Condition == | == Initial Condition == | ||
| - | :<math> u(x,0)=0 | + | :<math>u(x,0) = |
| - | + | \begin{cases} | |
| + | 0 & x \le 0 \\ | ||
| + | 1 & x > 0 | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
== Boundary condition == | == Boundary condition == | ||
| - | u | + | :<math>u(0,t)=0</math> |
== Exact solution == | == Exact solution == | ||
| - | :<math> u(x,t)=0 | + | :<math>u(x,t) = |
| - | + | \begin{cases} | |
| - | + | 0 & x \le 0 \\ | |
| + | x/t & 0 < x < t \\ | ||
| + | 1 & \mbox{otherwise} | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | |||
== Numerical method == | == Numerical method == | ||
| + | |||
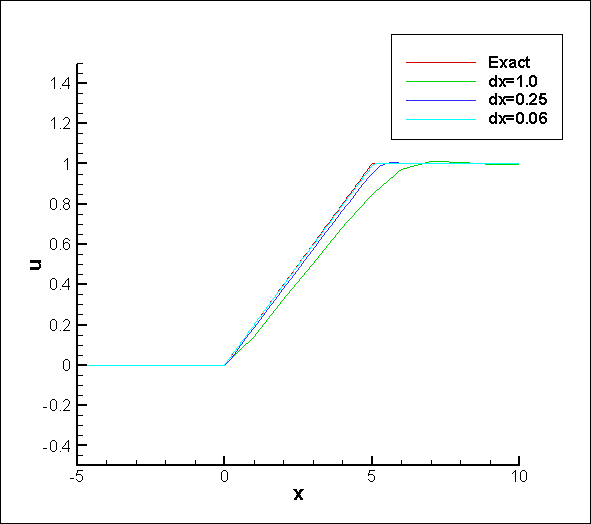
== Results == | == Results == | ||
[[Image:Nonlinear_1d.png]] | [[Image:Nonlinear_1d.png]] | ||
== Reference == | == Reference == | ||
Revision as of 23:28, 25 December 2005
Contents |

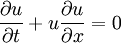
![x \in \left[-5,10\right]](/W/images/math/7/3/e/73ed4ae377158226e8d72ac9274b52a9.png)