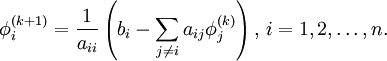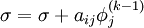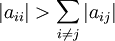Jacobi method
From CFD-Wiki
(Added more material) |
(Convergence, link to Wikipedia) |
||
| Line 32: | Line 32: | ||
:: check if convergence is reached | :: check if convergence is reached | ||
: end (k-loop) | : end (k-loop) | ||
| + | |||
| + | ==Convergence== | ||
| + | It is proven that if the absolute value of the diagonal term is always greater than the sum of the absolute values of other term in the row: | ||
| + | :<math>\left | a_{ii} \right | > \sum_{i \ne j} {\left | a_{ij} \right |} </math> | ||
| + | then the method always converge. | ||
| + | |||
| + | Usually, but not always, the method converges even if this condition is not satisfied, but the diagonal terms in the matrix are greater by the absolute values than the other terms. | ||
| + | |||
| + | ==External link== | ||
| + | *[http://en.wikipedia.org/wiki/Jacobi_method Wikipedia article] | ||
Revision as of 23:21, 13 February 2006
Contents |
Introduction
We seek the solution to set of linear equations:
In matrix terms, the definition of the Jacobi method can be expressed as :
where  ,
, 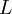 , and
, and 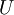 represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix
represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix 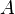 and
and 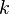 is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
Note that the computation of 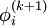 requires each element in
requires each element in 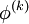 except itself. Then, unlike in the Gauss-Seidel method, we can't overwrite
except itself. Then, unlike in the Gauss-Seidel method, we can't overwrite 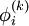 with
with 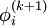 , as that value will be needed by the rest of the computation. This is the most meaningful difference between the Jacobi and Gauss-Seidel methods. The minimum ammount of storage is two vectors of size
, as that value will be needed by the rest of the computation. This is the most meaningful difference between the Jacobi and Gauss-Seidel methods. The minimum ammount of storage is two vectors of size 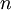 , and explicit copying will need to take place.
, and explicit copying will need to take place.
Algorithm
Chose an initial guess 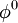 to the solution
to the solution
- for k := 1 step 1 untill convergence do
- for i := 1 step until n do
-
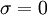
- for j := 1 step until n do
- if j != i then
-
- end if
- if j != i then
- end (j-loop)
-
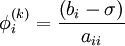
-
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (k-loop)
Convergence
It is proven that if the absolute value of the diagonal term is always greater than the sum of the absolute values of other term in the row:
then the method always converge.
Usually, but not always, the method converges even if this condition is not satisfied, but the diagonal terms in the matrix are greater by the absolute values than the other terms.

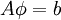
![\phi^{(k+1)} = D^{ - 1} \left[\left( {L + U} \right)\phi^{(k)} + b\right]](/W/images/math/2/5/1/251a2f655111e185ad6346ba43ad3117.png)