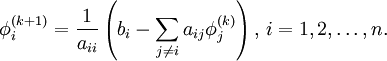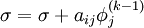Jacobi method
From CFD-Wiki
(Added more material) |
|||
| Line 1: | Line 1: | ||
| + | == Introduction == | ||
| + | |||
We seek the solution to set of linear equations: <br> | We seek the solution to set of linear equations: <br> | ||
| - | :<math> A \ | + | :<math> A \phi = b </math> <br> |
In matrix terms, the definition of the Jacobi method can be expressed as : <br> | In matrix terms, the definition of the Jacobi method can be expressed as : <br> | ||
| - | <math> | + | :<math> |
| - | \phi^{(k)} = D^{ - 1} \left( {L + U} \right)\phi^{(k | + | \phi^{(k+1)} = D^{ - 1} \left[\left( {L + U} \right)\phi^{(k)} + b\right] |
</math><br> | </math><br> | ||
| - | |||
| - | === Algorithm | + | where <math>D</math>, <math>L</math>, and <math>U</math> represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix <math>A</math> and <math>k</math> is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used: |
| - | + | ||
| - | + | :<math> | |
| + | \phi^{(k+1)}_i = \frac{1}{a_{ii}} \left(b_i -\sum_{j\ne i}a_{ij}\phi^{(k)}_j\right),\, i=1,2,\ldots,n. | ||
| + | </math> | ||
| + | |||
| + | Note that the computation of <math>\phi^{(k+1)}_i</math> requires each element in <math>\phi^{(k)}</math> except itself. Then, unlike in the [[Gauss-Seidel method]], we can't overwrite <math>\phi^{(k)}_i</math> with <math>\phi^{(k+1)}_i</math>, as that value will be needed by the rest of the computation. This is the most meaningful difference between the Jacobi and Gauss-Seidel methods. The minimum ammount of storage is two vectors of size <math>n</math>, and explicit copying will need to take place. | ||
| + | |||
| + | == Algorithm == | ||
| + | Chose an initial guess <math>\phi^{0}</math> to the solution <br> | ||
: for k := 1 step 1 untill convergence do <br> | : for k := 1 step 1 untill convergence do <br> | ||
:: for i := 1 step until n do <br> | :: for i := 1 step until n do <br> | ||
| Line 24: | Line 32: | ||
:: check if convergence is reached | :: check if convergence is reached | ||
: end (k-loop) | : end (k-loop) | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
Revision as of 01:22, 19 December 2005
Introduction
We seek the solution to set of linear equations:
In matrix terms, the definition of the Jacobi method can be expressed as :
where 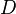 ,
, 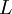 , and
, and 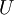 represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix
represent the diagonal, lower triangular, and upper triangular parts of the coefficient matrix 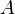 and
and 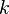 is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
is the iteration count. This matrix expression is mainly of academic interest, and is not used to program the method. Rather, an element-based approach is used:
Note that the computation of 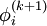 requires each element in
requires each element in 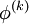 except itself. Then, unlike in the Gauss-Seidel method, we can't overwrite
except itself. Then, unlike in the Gauss-Seidel method, we can't overwrite 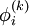 with
with 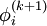 , as that value will be needed by the rest of the computation. This is the most meaningful difference between the Jacobi and Gauss-Seidel methods. The minimum ammount of storage is two vectors of size
, as that value will be needed by the rest of the computation. This is the most meaningful difference between the Jacobi and Gauss-Seidel methods. The minimum ammount of storage is two vectors of size 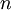 , and explicit copying will need to take place.
, and explicit copying will need to take place.
Algorithm
Chose an initial guess 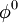 to the solution
to the solution
- for k := 1 step 1 untill convergence do
- for i := 1 step until n do
-
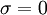
- for j := 1 step until n do
- if j != i then
-
- end if
- if j != i then
- end (j-loop)
-
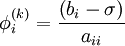
-
- end (i-loop)
- check if convergence is reached
- for i := 1 step until n do
- end (k-loop)

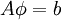
![\phi^{(k+1)} = D^{ - 1} \left[\left( {L + U} \right)\phi^{(k)} + b\right]](/W/images/math/2/5/1/251a2f655111e185ad6346ba43ad3117.png)