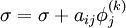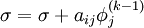CFD Online Logo CFD Online URL
www.cfd-online.com
[Sponsors]
Home > Wiki > Successive over-relaxation method - SOR

Successive over-relaxation method - SOR

From CFD-Wiki

(Difference between revisions)
Jump to: navigation, search
(fixed dot product notation)
(towards a uniform notation for linear systems : A*Phi = B)
Line 1: Line 1:
We seek the solution to set of linear equations: <br>
We seek the solution to set of linear equations: <br>
-
:<math> A \cdot X = Q </math> <br>
+
:<math> A \cdot \Phi = B </math> <br>
-
For the given matrix '''A''' and vectors '''X''' and '''Q'''. <br>
 
In matrix terms, the definition of the SOR method can be expressed as : <br>
In matrix terms, the definition of the SOR method can be expressed as : <br>
<math>  
<math>  
-
x^{(k)}  = \left( {D - \omega L} \right)^{ - 1} \left( {\omega U + \left( {1 - \omega } \right)D} \right)x^{(k - 1)}  + \omega \left( {D - \omega L} \right)^{ - 1} q
+
\phi^{(k)}  = \left( {D - \omega L} \right)^{ - 1} \left( {\omega U + \left( {1 - \omega } \right)D} \right)\phi^{(k - 1)}  + \omega \left( {D - \omega L} \right)^{ - 1} B
</math><br>
</math><br>
Where '''D''','''L''' and '''U''' represent the diagonal, lower triangular and upper triangular matrices of coefficient matrix '''A''' and k is iteration counter.<br>
Where '''D''','''L''' and '''U''' represent the diagonal, lower triangular and upper triangular matrices of coefficient matrix '''A''' and k is iteration counter.<br>
-
<math> \omega </math> is extrapolation factor. <br>
+
<math> \omega </math> is a relaxation factor. <br>
The pseudocode for the SOR algorithm: <br>
The pseudocode for the SOR algorithm: <br>
Line 15: Line 14:
=== Algorithm ===
=== Algorithm ===
----
----
-
:    Chose an intital guess <math>X^{0}</math> to the solution <br>
+
:    Chose an intital guess <math>\Phi^{0}</math> to the solution <br>
:    for k := 1 step 1 untill convergence do <br>
:    for k := 1 step 1 untill convergence do <br>
::  for i := 1 step until n do <br>
::  for i := 1 step until n do <br>
:::  <math> \sigma = 0 </math> <br>
:::  <math> \sigma = 0 </math> <br>
:::  for j := 1 step until i-1 do <br>
:::  for j := 1 step until i-1 do <br>
-
::::      <math> \sigma  = \sigma  + a_{ij} x_j^{(k)} </math>
+
::::      <math> \sigma  = \sigma  + a_{ij} \phi_j^{(k)} </math>
:::    end (j-loop) <br>
:::    end (j-loop) <br>
:::  for j := i+1 step until n do <br>
:::  for j := i+1 step until n do <br>
-
::::      <math> \sigma  = \sigma  + a_{ij} x_j^{(k-1)} </math>
+
::::      <math> \sigma  = \sigma  + a_{ij} \phi_j^{(k-1)} </math>
:::    end (j-loop) <br>
:::    end (j-loop) <br>
-
:::    <math>  \sigma  = {{\left( {q_i - \sigma } \right)} \over {a_{ii} }} </math>
+
:::    <math>  \sigma  = {{\left( {b_i - \sigma } \right)} \over {a_{ii} }} </math>
-
:::    <math> x_i^{(k)}  = x_i^{(k - 1)}  + \omega \left( {\sigma  - x_i^{k - 1} } \right)  </math>
+
:::    <math> \phi_i^{(k)}  = \phi_i^{(k - 1)}  + \omega \left( {\sigma  - \phi_i^{k - 1} } \right)  </math>
::  end (i-loop)
::  end (i-loop)
::  check if convergence is reached
::  check if convergence is reached

Revision as of 20:49, 15 December 2005

We seek the solution to set of linear equations:

A \cdot \Phi = B

In matrix terms, the definition of the SOR method can be expressed as :
\phi^{(k)} = \left( {D - \omega L} \right)^{ - 1} \left( {\omega U + \left( {1 - \omega } \right)D} \right)\phi^{(k - 1)} + \omega \left( {D - \omega L} \right)^{ - 1} B
Where D,L and U represent the diagonal, lower triangular and upper triangular matrices of coefficient matrix A and k is iteration counter.
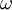\omega is a relaxation factor.

The pseudocode for the SOR algorithm:

Algorithm

Chose an intital guess 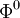\Phi^{0} to the solution
for k := 1 step 1 untill convergence do
for i := 1 step until n do
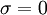
\sigma = 0
for j := 1 step until i-1 do
\sigma = \sigma + a_{ij} \phi_j^{(k)}
end (j-loop)
for j := i+1 step until n do
\sigma = \sigma + a_{ij} \phi_j^{(k-1)}
end (j-loop)
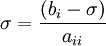
\sigma = {{\left( {b_i - \sigma } \right)} \over {a_{ii} }}
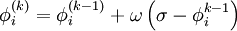
\phi_i^{(k)} = \phi_i^{(k - 1)} + \omega \left( {\sigma - \phi_i^{k - 1} } \right)
end (i-loop)
check if convergence is reached
end (k-loop)


Return to Numerical Methods

Retrieved from "https://openfoam.cfd-online.com/Wiki/Successive_over-relaxation_method_-_SOR"
My wiki