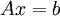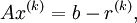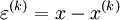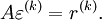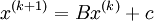Iterative methods
From CFD-Wiki
m (Basic concept of iterative solutions moved to Iterative methods) |
m |
||
| Line 1: | Line 1: | ||
| - | + | We seek the solution to the linear system of equations <br> | |
| - | :<math> | + | :<math> Ax = b </math> <br> |
| - | After ''k'' iterations we obtain an | + | Iterative methods, unlike direct methods, generate a sequence of approximate solutions to the system that (hopefully) converges to the exact solution. After ''k'' iterations, we obtain an approximation to the exact solution as: <br> |
| - | :<math> Ax^{(k)} = | + | :<math> Ax^{(k)} = b - r^{(k)}, </math><br> |
where <math> r^{(k)} </math> is the residual after ''k'' iterations. <br> | where <math> r^{(k)} </math> is the residual after ''k'' iterations. <br> | ||
| - | Defining | + | Defining <br> |
:<math> \varepsilon ^{(k)} = x - x^{(k)} </math> <br> | :<math> \varepsilon ^{(k)} = x - x^{(k)} </math> <br> | ||
| - | as the difference between the exact and approaximate solution | + | as the difference between the exact and approaximate solution, we obtain <br> |
| - | we obtain | + | :<math> A\varepsilon ^{(k)} = r^{(k)}. </math> <br> |
| - | :<math> A\varepsilon ^{(k)} = r^{(k)} </math> <br> | + | The purpose of iterations is to drive this residual to zero. |
| - | + | ||
===Stationary Iterative Methods=== | ===Stationary Iterative Methods=== | ||
| Line 39: | Line 38: | ||
#BiConjugate Gradient Stabilized (Bi-CGSTAB) | #BiConjugate Gradient Stabilized (Bi-CGSTAB) | ||
#Chebyshev Iteration | #Chebyshev Iteration | ||
| - | |||
| - | |||
| - | |||
| - | |||
Revision as of 00:00, 19 December 2005
We seek the solution to the linear system of equations
Iterative methods, unlike direct methods, generate a sequence of approximate solutions to the system that (hopefully) converges to the exact solution. After k iterations, we obtain an approximation to the exact solution as:
where 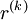 is the residual after k iterations.
is the residual after k iterations.
Defining
as the difference between the exact and approaximate solution, we obtain
The purpose of iterations is to drive this residual to zero.
Stationary Iterative Methods
Iterative methods that can be expressed in the simple form
when neither B nor c depend upon the iteration count (k), the iterative method is called stationary iterative method. Some of the stationary iterative methods are
- Jacobi method
- Gauss-Seidel method
- Successive Overrelaxation (SOR) method and
- Symmetric Successive Overrelaxation (SSOR) method
The convergence of such iterative methods can be investigated using the Fixed point theorem.
Nonstationary Iterative Methods
When during the iterations B and c changes during the iterations, the method is called Nonstationary Iterative Method. Typically, constants B and c are computed by taking inner products of residuals or other vectors arising from the iterative method.
Some examples are:
- Conjugate Gradient Method (CG)
- MINRES and SYMMLQ
- Generalized Minimal Residual (GMRES)
- BiConjugate Gradient (BiCG)
- Quasi-Minimal Residual (QMR)
- Conjugate Gradient Squared Method (CGS)
- BiConjugate Gradient Stabilized (Bi-CGSTAB)
- Chebyshev Iteration