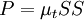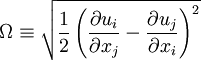Kato-Launder modification
From CFD-Wiki
| Line 70: | Line 70: | ||
==Production term modification== | ==Production term modification== | ||
| - | The proposal by Kato and Launder is to replace one of the strain-rates, <math>S</math>, in the turbulent production term | + | The proposal by Kato and Launder is to replace one of the strain-rates, <math>S</math>, in the turbulent production term with the vorticity, <math>\Omega</math>. Hence, the Kato-Launder modified production is: |
| - | + | ||
| - | + | ||
:<math> | :<math> | ||
| Line 87: | Line 85: | ||
:<math> | :<math> | ||
| - | + | \Omega \equiv \sqrt{\frac{1}{2} \left( \frac{\partial u_i}{\partial x_j} - \frac{\partial u_j}{\partial x_i} \right)^2 } | |
</math> | </math> | ||
| - | In pure shear-flows like boundary-layers and wakes the Kato-Launder modified production term will give exactly the same result as the unmodified production term | + | In pure shear-flows like boundary-layers and wakes the Kato-Launder modified production term will give exactly the same result as the unmodified production term. However, outside of boundary-layers and wakes the Kato-Launder modified production term will give very different results. Essentially what it does is to turn off the turbulent production outside of the boundary-layers and wakes. This has the good effect that |
==References== | ==References== | ||
{{reference-paper|author=Kato, M. and Launder, B. E.|year=1993|title=The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders|rest=Proc. 9th Symposium on Turbulent Shear Flows, Kyoto, August 1993, pp. 10.4.1-10.4.6}} | {{reference-paper|author=Kato, M. and Launder, B. E.|year=1993|title=The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders|rest=Proc. 9th Symposium on Turbulent Shear Flows, Kyoto, August 1993, pp. 10.4.1-10.4.6}} | ||
Revision as of 15:51, 8 December 2005
The Kato-Launder modification is an ad-hoc modification of the turbulent production term in the k equation. The main purpose of the modification is to reduce the tendency that two-equation models have to over-predict the turbulent production in regions with large normal strain, i.e. regions with strong acceleration or decelleration.
Basic equations
The transport equation for the turbulent energy, 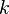 , used in most two-equation models can be written as:
, used in most two-equation models can be written as:
Where  is the turbulent production normally given by:
is the turbulent production normally given by:
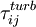 is the turbulent shear stress tensor given by the Boussinesq assumption:
is the turbulent shear stress tensor given by the Boussinesq assumption:
Where 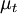 is the eddy-viscosity given by the turbluence model and
is the eddy-viscosity given by the turbluence model and 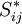 is the trace-less viscous strain-rate defined by:
is the trace-less viscous strain-rate defined by:
In incompressible flows, where 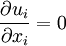 , the production term
, the production term  can be rewritten as:
can be rewritten as:
Hence
Where
Production term modification
The proposal by Kato and Launder is to replace one of the strain-rates, 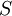 , in the turbulent production term with the vorticity,
, in the turbulent production term with the vorticity, 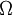 . Hence, the Kato-Launder modified production is:
. Hence, the Kato-Launder modified production is:
Where
and
In pure shear-flows like boundary-layers and wakes the Kato-Launder modified production term will give exactly the same result as the unmodified production term. However, outside of boundary-layers and wakes the Kato-Launder modified production term will give very different results. Essentially what it does is to turn off the turbulent production outside of the boundary-layers and wakes. This has the good effect that
References
Kato, M. and Launder, B. E. (1993), "The Modeling of Turbulent Flow Around Stationary and Vibrating Square Cylinders", Proc. 9th Symposium on Turbulent Shear Flows, Kyoto, August 1993, pp. 10.4.1-10.4.6.

![\frac{\partial}{\partial t} \left( \rho k \right) +
\frac{\partial}{\partial x_j}
\left[
\rho k u_j - \left( \mu + \frac{\mu_t}{\sigma_k} \right)
\frac{\partial k}{\partial x_j}
\right]
=
P - \rho \epsilon - \rho D](/W/images/math/8/d/7/8d787db6600e44ff6855992620431595.png)
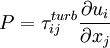
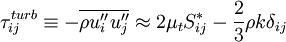
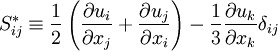
![\begin{matrix}
P & = & \tau_{ij}^{turb} \frac{\partial u_i}{\partial x_j} \\
\ & = & \left[ 2 \mu_t S_{ij}^* - \frac{2}{3} \rho k \delta_{ij} \right] \frac{\partial u_i}{\partial x_j} \\
\ & = & \left[ 2 \mu_t \left( \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} +
\frac{\partial u_j}{\partial x_i} \right) - \frac{1}{3} \frac{\partial u_k}{\partial x_k} \delta_{ij} \right)
- \frac{2}{3} \rho k \delta_{ij}
\right] \frac{\partial u_i}{\partial x_j} \\
\ & \approx & \mu_t \left(\frac{\partial u_i}{\partial x_j} +
\frac{\partial u_j}{\partial x_i} \right) \frac{\partial u_i}{\partial x_j} \\
\ & = & \mu_t \frac{1}{2} \left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right)
\left(\frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) \\
\end{matrix}](/W/images/math/c/2/e/c2edca17cad100ee94b91f1ebc9516c5.png)