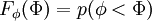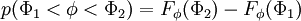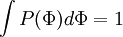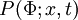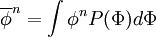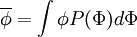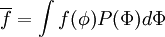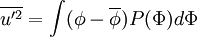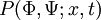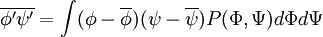Probability density function
From CFD-Wiki
m (Probability Density Function moved to Probability density function) |
|||
| Line 29: | Line 29: | ||
The PDF of any stochastic variable depends "a-priori" on space and time. | The PDF of any stochastic variable depends "a-priori" on space and time. | ||
:<math> P(\Phi;x,t) </math> | :<math> P(\Phi;x,t) </math> | ||
| + | |||
| + | From the PDF of a variable, one can define its <math> n </math>th moment as | ||
| + | |||
| + | :<math> | ||
| + | \overline{\phi}^n = \int \phi^n P(\Phi) d \Phi | ||
| + | </math> | ||
| + | |||
| + | the <math> n = 1 </math> case is called the "mean". | ||
| + | |||
| + | :<math> | ||
| + | \overline{\phi} = \int \phi P(\Phi) d \Phi | ||
| + | </math> | ||
| + | |||
| + | Similarly the mean of a function can be obtained as | ||
| + | |||
| + | :<math> | ||
| + | \overline{f} = \int f(\phi) P(\Phi) d \Phi | ||
| + | </math> | ||
| + | |||
| + | Where the second central moment is called the "variance" | ||
| + | |||
| + | :<math> | ||
| + | \overline{u'^2} = \int (\phi-\overline{\phi}) P(\Phi) d \Phi | ||
| + | </math> | ||
| + | |||
| + | For two variables (or more) a joint-PDF of <math> \phi </math> and <math> \psi </math> is defined | ||
| + | :<math> P(\Phi,\Psi;x,t) </math> | ||
| + | |||
| + | and the marginal PDF's are obatined by integration over the sample space of one variable. | ||
| + | :<math> | ||
| + | P(\Phi) = \int P(\Phi,\Psi) d\Psi | ||
| + | </math> | ||
| + | |||
| + | For two variables the correlation is given by | ||
| + | |||
| + | :<math> | ||
| + | \overline{\phi' \psi'} = \int (\phi-\overline{\phi}) (\psi-\overline{\psi}) P(\Phi,\Psi) d \Phi d\Psi | ||
| + | </math> | ||
| + | |||
| + | This term often appears in turbulent flows the averaged Navier-Stokes (with <math> u, v </math>) and is unclosed. | ||
| + | |||
| + | Using Bayes' theorem a joint-pdf can be expressed as | ||
| + | :<math> | ||
| + | P(\Phi,\Psi) = P(\Phi|\Psi) P(\Psi) | ||
| + | </math> | ||
| + | where <math> P(\Phi|\Psi) </math> is the conditional PDF. | ||
| + | |||
| + | If two variables are uncorrelated then they are statistically independent and their joint PDF can be expressed as a product of their marginal PDFs. | ||
| + | :<math> | ||
| + | P(\Phi,\Psi)= P(\Phi) P(\Psi) | ||
| + | </math> | ||
Revision as of 11:31, 18 October 2005
Stochastic methods use distribution functions to decribe the fluctuacting scalars in a turbulent field.
The distribution function 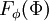 of a scalar
of a scalar 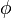 is the probability
is the probability
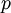 of finding a value of
of finding a value of 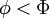
The probability of finding 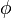 in a range
in a range 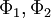 is
is
The probability density function (PDF) is
where 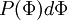 is the probability of
is the probability of 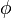 being in the range
being in the range 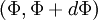 . It follows that
. It follows that
Integrating over all the possible values of 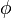 .
The PDF of any stochastic variable depends "a-priori" on space and time.
.
The PDF of any stochastic variable depends "a-priori" on space and time.
From the PDF of a variable, one can define its 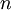 th moment as
th moment as
the 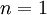 case is called the "mean".
case is called the "mean".
Similarly the mean of a function can be obtained as
Where the second central moment is called the "variance"
For two variables (or more) a joint-PDF of 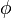 and
and 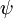 is defined
is defined
and the marginal PDF's are obatined by integration over the sample space of one variable.
For two variables the correlation is given by
This term often appears in turbulent flows the averaged Navier-Stokes (with 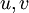 ) and is unclosed.
) and is unclosed.
Using Bayes' theorem a joint-pdf can be expressed as
where 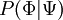 is the conditional PDF.
is the conditional PDF.
If two variables are uncorrelated then they are statistically independent and their joint PDF can be expressed as a product of their marginal PDFs.