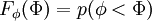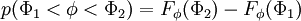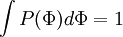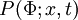Probability density function
From CFD-Wiki
(Difference between revisions)
m |
|||
| Line 6: | Line 6: | ||
:<math> | :<math> | ||
| - | F_\phi(\Phi) = p(phi < \Phi) | + | F_\phi(\Phi) = p(\phi < \Phi) |
</math> | </math> | ||
| Line 13: | Line 13: | ||
:<math> | :<math> | ||
| - | p(\Phi_1 <phi < \Phi_2) = F_\phi(\Phi_2)-F_\phi(\Phi_1) | + | p(\Phi_1 <\phi < \Phi_2) = F_\phi(\Phi_2)-F_\phi(\Phi_1) |
</math> | </math> | ||
Revision as of 12:12, 17 October 2005
Stochastic methods use distribution functions to decribe the fluctuacting scalars in a turbulent field.
The distribution function 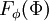 of a scalar
of a scalar 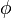 is the probability
is the probability
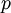 of finding a value of
of finding a value of 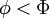
The probability of finding 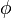 in a range
in a range 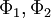 is
is
The probability density function (PDF) is
where 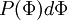 is the probability of
is the probability of 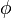 being in the range
being in the range 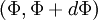 . It follows that
. It follows that
Integrating over all the possible values of 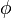 .
The PDF of any stochastic variable depends "a-priori" on space and time.
.
The PDF of any stochastic variable depends "a-priori" on space and time.